What is zkSNARKs: Spooky Moon Math

Zero Knowledge proofs came about in 1980’s thanks to the work of MIT researchers Shafi Goldwasser, Silvio Micali and Charles Rackoff. They were working on problems related to interactive proof systems, where a Prover exchanges messages with a Verifier (more on provers and verifiers later) to convince them that they have a knowledge of a certain proof without declaring what that knowledge is.

Before they made their landmark discovery, most proof systems were based on the “soundness” properties of the proof system. It was always assumed that the “prover” could be the malicious one in any scenario wherein they will try to fool the verifier. These 3 researchers flipped the idea on its head by questioning the morality of the verifier instead of the prover. The question they asked was, how can anyone know for sure that the verifier won’t leak the knowledge and there were also concerns raised as to the amount of knowledge about the prover that the verifier will get to know during the process of verification.

There are various real world consequences of this conundrum and one of the most famous ones have to do with password protection. Suppose you want to login to a website using a password. The standard protocol is that the client (you) will write in their password and send it to the server, the server will then hash the password and equate it to the hash that they have stored in their system. If the values match up, then you can enter the system.

Can you see the huge flaw in this system right?

The server has the plaintext version of your password, and your privacy is at the mercy of the server (the verifier in this scenario). If the server gets compromised or attacked, then your password will be with the malicious party and the consequences could be dire. In order to counter these scenarios, zero knowledge proofs are absolutely essential and path breaking in every sense.

There are two parties when it comes to a zero knowledge proof (as stated above), the prover and the verifier. Zero knowledge states that a prover can prove to the verifier that they possess a certain knowledge without telling them what that knowledge actually is

Properties of a zero knowledge proof

For a ZKP to work it needs to satisfy certain parameters:

Completeness: If the statement is true then an honest verifier can be convinced of it by an honest prover.
Soundness: If the prover is dishonest, they can’t convince the verifier of the soundness of the statement by lying.
Zero-Knowledge: If the statement is true, the verifier will have no idea what the statement actually is.

So now that we have a basic idea of what a zero-knowledge proof is, let’s check out some examples of it before we dive deep into zk-snarks and its application in the blockchain.

Case #1 Alibaba’s Cave

In this example, the prover (P) is saying to the verifier(V) that they know the password of the secret door at the back of the cave and they want to prove it to the verifier without actually telling them the password.

So this is what it looks like:

Save

Image courtesy: Scott Twombly (YouTube channel)

The Prover goes down any of the paths A and B, suppose they initially decide to go through path A and reach the secret door at the back. When they do so, the verifier V comes in at the entrance, with no knowledge of which path the prover actually took and declares that they want to see the prover appear from path B.

In the diagram, as you can see, the prover does indeed appear in path B. But what if this was dumb luck? What if the prover didn’t know the pass code, and took the path B, was stuck at the door and by sheer fortune, the verifier told him to appear from path B, the one they were originally on anyway?

So, to test the validity, the experiment is done multiple times. If the prover can appear at the correct path every single time, it proves to the verifier that the prover indeed knows the password even though the verifier doesn’t know what the password actually is.

Let’s see how the three properties of zero knowledge are satisfied in this example:

Completeness: Since the statement was true, the honest prover convinced the honest verifier.
Soundness: If the prover was dishonest, they couldn’t have fooled the verifier because the test was done multiple times. Eventually, the prover’s luck had to run out.
Zero-Knowledge: The verifier never knew what the password was, but was convinced that the prover had possession of it.

Case #2 Finding Waldo

Remember finding Waldo?

Of course, you do, you must have seen it somewhere, either in real life or online. For those who don’t know, Finding Waldo is a game where you have to find “Waldo” among a sea of people. It is a simple “Spot the guy” game. Just to give you a basic idea, this is what the game looks like:

Save

Image courtesy: Youtube (IntoConnection)

And the idea is to find Waldo who looks like this:

Image courtesy: Pinterest

Seems pretty straightforward right? Find this guy among the sea of other people that you see in the game. Ok, so where does the concept of Zero Knowledge come in here? Imagine there are two people Anna and Carl. Anna tells Carl that she knows where Wally is but she doesn’t want to show him where exactly he is. So, how can she prove to him that she has found Wally without showing his exact position?

There was, an interesting paper by Naor, Naor and Reingold which shows two Zero Knowledge solutions to this problem. There is a “Mid-Tech Solution” and a “Low-Tech Solution”. Let’s discuss both of them.

Mid-Tech Solution

The reason why this solution is “mid-tech” is because our prover and verifier need access to a photocopy machine to make this work. So this is how it goes. First, Anna and Carl would make a photocopy of the original game. Then Anna, whilst making sure that Carl isn’t looking, will cut out Waldo from the photocopy and then destroy the leftovers. After that she can show the Waldo cut out to Carl and prove that she did know where Waldo was after all without pinpointing his exact location to Carl.

There are problems with this solution. While it does fulfill the “Zero Knowledge” criteria, it doesn’t fulfill the “Soundness” criteria. There are many ways that Anna could have cheated here. She could have had a random Waldo cut out with her from the very beginning and could have just shown it to Carl without actually knowing where Waldo was. So what is the solution to this?

The solution to this is meticulous and careful testing. Firstly, Anna and Carl will take a photocopy of the game. Then Carl will draw a distinctive pattern at the back of the photocopy. After that, Carl will escort Anna to a room where she will be isolated and have no chance of cheating whatsoever. If Anna comes out with a cutout of Waldo, then Carl can be convinced that she actually knew where Waldo was without revealing the solution. They can repeat this experiment multiple times and Carl can compare the different cutouts of Waldo to be even further sure about the validity of Anna’s claim.

Low-Tech Solution

This solution required very basic equipment. The idea is simple. Get a huge cardboard, one that is twice the size of the game and cut out a small rectangle on it. Now, when Carl isn’t looking, Anna can move the cardboard on the game in such a way that the rectangle is directly on top of Waldo. Now, she can tell Carl to have a look and this is what he will see:

Save

Image Courtesy: Applied Kid Cryptography by Naor And Reingold

So, while Carl may get a very basic idea of where Waldo actually can be, he doesn’t know the exact location. Anna has hence proved to Carl that she knows where Waldo is without pinpointing his exact location.

Case #3: Sudoku

Another great application of zero knowledge is in Sudoku. For those who don’t know, Sudoku is a Japanese puzzle where you get a 9X9 table which looks something like this:

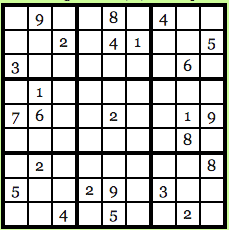
Image courtesy: Computational Complexity Blog.

The idea is to fill up every row, every column and every 3X3 block with numbers from 1-9 and no number should repeat itself. So, the solution for the puzzle above looks like this:

Image courtesy: Computational Complexity Blog.

As you can see, every row, column, and 3X3 block are unique and not a single number has been repeated. Let’s go back to our old friends Anna and Carl. Anna has found the solution to the Sudoku puzzle and Carl, skeptic that he is doesn’t believe her and wants Anna to prove that she does indeed know the solution. Anna wants to prove her honesty, but at the same time, she doesn’t want Carl to know the exact solution of the puzzle. How will she go about it? Anna is going to use Zero Knowledge to prove the validity of her claim.

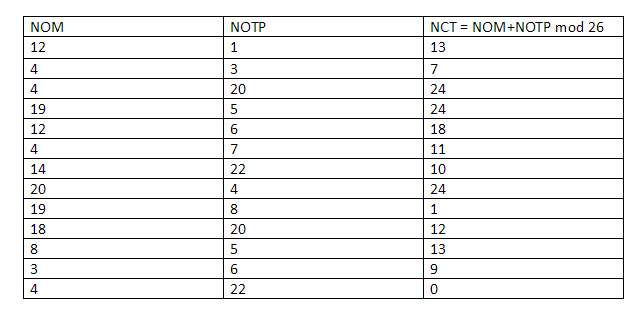
Firstly, Carl will run the Sudoku solution through a computer program which has been verified, to be honest and the program will run the numbers through a randomly chosen substitution cipher. Say, for this particular problem the cipher that the program has chosen is this:

Save

The chosen program and cipher is such that each digit has the same chance of being transmuted into its substitution as any other number. Basically, 1 has as much chance of being transmuted as 3 and 4 have as much chance of being transmuted as 9 and so on and so forth. So, using this cipher gives us the following solution to the puzzle above:

Image courtesy: Computational Complexity Blog.

Anna gets the transmuted solution now, keep in mind that Carl still doesn’t know what the original solution was and he doesn’t possess the transmuted solution either. So, what Anna does now is that she hides all the numbers in the puzzle by using a “lockbox mechanism”, basically Carl won’t be able to see any of the numbers and will see an empty 9X9 grid in front of him.

Carl now has 28 choices in front of him:

Reveal a row.
Reveal a column.
Reveal a 3X3 box.
Reveal the transmuted version of the original puzzle.

Suppose Carl wants to know what the third row looks like:

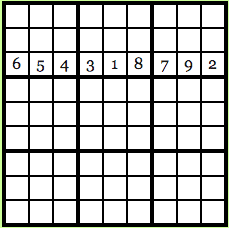
Image courtesy: Computational Complexity Blog.

This is what he will see. Carl will see that every number in the row is unique and since every possible number in the original solution had the same probability of being transmuted via the cipher, Carl will have no clue as to what the original solution is.

Now suppose, Carl decides to take the last option and wants to see what the original puzzle in looks like when transmuted:

Image courtesy: Computational Complexity Blog.

Once again, since the cipher was chosen at random and all the numbers have the same probability of being transmuted, Carl will have no idea what the original solution is. Carl can now go through all 28 of his choices and eventually he will be satisfied with the validity of Anna’s statement.

Why?

Because, if Anna was indeed cheating, there is no way that she could have found a cipher to give unique solutions for all 28 of Carl’s choices. If Carl just chose one option, Anna’s chances of getting away with cheating are 27/28. BUT if Carl chose to do random test multiple times, suppose he chooses to test it 150 times, Anna’s choice of getting away with cheating drops down to (27/28) ^150 which is < 0.5%.

So, let’s check out the zero knowledge properties of this scenario:

Completeness: The cipher program being used has been verified, to be honest, and both Anna and Carl are following protocol.
Soundness: If Carl does random tests 150 times, Anna’s chances of getting away with cheating is < 0.5%.
Zero-Knowledge: Anna never had to reveal to Carl what the original solution was.

Proof vs Proof Of Statements

Now that we know the theoretical aspects of zero knowledge proofs and its application in various examples, what is its practical application in blockchain? Why is everyone raving about Zcash for implementing ZKP (zero knowledge proofs) and why is everyone excited about Ethereum doing the same? Before we expand on that, it is important to know one more important theoretical concept.

What exactly are we proving by using ZKP? In a broad spectrum, there are two statements that you can prove by using ZKP. Proofs aka facts and proof of knowledge.

Proofs: These are the intrinsic truths about the universe that you may want to prove via ZKP. Eg. “number X belongs to a group Y”.

Proof of knowledge: You may also want to prove that you have knowledge of a particular idea without revealing what that particular knowledge is. As can be seen in the examples of Sudoku, Waldo and Alibaba’s cave given above.

It is important to note the difference between these two because they are completely different. In the cryptocurrency world, we are mostly focused around “proof of knowledge”. One of the most important breakthroughs in proving proof of knowledge via zero knowledge proof came when Claus-Peter Schnorr in the 1980s came up with the Schnorr identification protocol. This protocol lays the basics of modern key signature cryptography and displays how Zero-knowledge can be seamlessly integrated into modern cryptographical practices.

The Schnorr Identification Protocol

To understand what the Schnorr Identification is about let’s bring back our old friends Anna and Carl. Anna has announced to the world that she has a public key and can accept and receive information through it. Carl, always the skeptic, thinks that Anna is lying. The only way that Anna can prove her honesty is by showing her private key to Carl, but she doesn’t want to reveal her private key.

So, how will Anna reveal her knowledge of her private key without revealing it? This is where the Schnorr protocol comes in. Before we even begin to understand how the protocol works, there are certain parameters that you need to know:

p = Any prime number.
q= factor of p-1.
“a” such that a^q = 1 mod p.

Now keep in mind, in the Schnorr protocol, these 3 variables are global. Meaning anyone has knowledge of what these 3 variables for a particular scenario are.

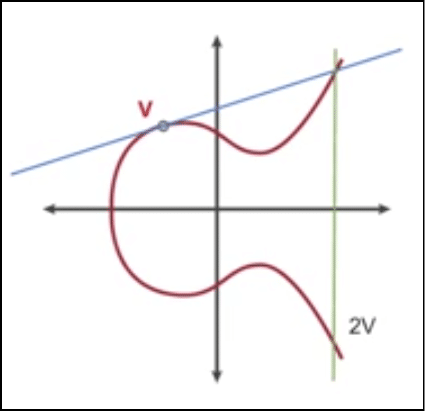
Now we come to the two keys, the secret private key that we will call “s” and the public key that we will call “v”.

s can be any value as long as 0<s<q.

v = a^-s mod q.

The public key “v” will be global and public knowledge along with p,q and a. However, ONLY Anna will have the knowledge of what “s” is, because that is her private key.

So, now that we have defined the variable, let’s see how the information exchange and the validity of Anna’s statement can work WITHOUT her revealing what the private key is.

Anna signs and sends an encrypted message

Suppose Anna wants to send a message “M” to Carl encoded with her private key. How will she do it if she were to follow Schnorr’s protocol?

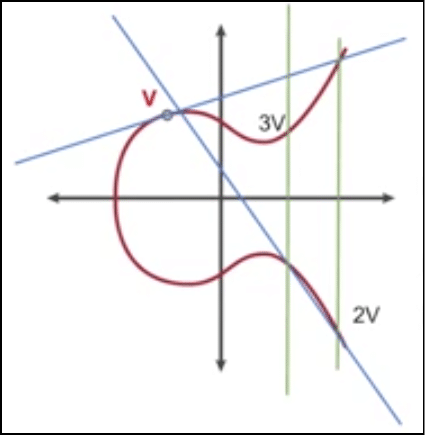
Firstly, she will choose a random number “r” such that 0<r<q.

Now she will compute a value x such that:

X= a^r mod p.

Now that she has computed the value of X, she is going concatenate this with the original message. What is concatenation? Suppose we have two strings “hello” and “world”. If we concatenate these two, then we will get “hello world”. Concatenation basically means adding two strings and making it one.

So, she is going to concatenate M and X to get M||X. and she is going to store the hash of this value in e.

Basically, e = H(M||X) where H() is the hash function.

Finally, when all this is done, she will do one final computation. She is going to get a value “y” such that:

y = (r + s*e) mod q

Now that all the computations are over, she is going to send the following pieces of information to Carl:

The message “M”.
The signatures e and y.

Carl receives the message and verifies Anna’s proof of knowledge

Now Carl has received the following pieces of information from Anna: The message (M) and the signatures (e and y).

Along with that, he has the following pieces of information that is known publicly to everyone:

Anna’s public key “v”.
The prime number that Anna chose “p”.
“q” which is the factor of “p-1” which Anna chose.
And the “a” such that a^q = 1 mod p, this also Anna chose.

Now, Carl will have to compute X’ such that:

X’ = a^y * v^e mod p.

Now let’s do some simple substitution:

We know that v = a^-s, let’s substitute that in the equation above and we get:

X’ = a^y * a^-se = a ^ (y-s*e).
Now we also know that y = r + s*e.
Which means: r = y-s*e.

Let’s substitute this value in the equation above:

We get: X’ = a^r.
As we have already seen above: X= a^r.
So technically: X = X’.

But Carl doesn’t know the value of “X” because he never received that value. All that he received are the following: The message M, the signatures (e and y) and the host of public variables (public key “v”, p ,q, and a).

He never received “X” but he knows that if Anna is speaking the truth then X’ has to be equal to X.

But, he does know the value of e and the message M.

So he is going to solve for e by doing the following:

e = H ( M||X’).

Note that earlier we solved for e by doing: H(M||X).

So, by that logic, if the two values of e come up to be the same then that means X = X’.

This also means that Anna did indeed have the private key all along and she was not lying.

So, let’s run this entire scenario through the three properties of zero knowledge proofs:

Completeness: Carl was convinced of Anna’s honesty because at the end X = X’.
Soundness: The plan was sound because the only way Anna could have proved her honesty was by using her private key. She couldn’t have lied about having the private key.
Zero Knowledge: Carl never found out what Anna’s private key was.

Schnorr’s protocol gives a very real world cryptographical application of zero knowledge proofs.

How to make zero knowledge proofs non-interactive?

With earlier zero-knowledge verification systems there was one big problem. For it to work, the prover and the verifier had to be online at the same time. In other words, the process was “interactive”. This made the entire system inefficient and almost impossible to scale up. The verifiers couldn’t possibly be online at the same time as provers all the time? There needed to be a system to make this more efficient.

In 1986, Fiat and Shamir invented the Fiat-Shamir heuristic and successfully changed the interactive zero-knowledge proof to non-interactive zero knowledge proof. This helped the entire protocol work without any interaction. The procedure behind it is very simple.

So, to give you an example, this is how zero knowledge proofs used to work before Fiat and Shamir.

Let’s prove this using simple discrete logarithms.

Anna wants to prove to Carl that she knows a value x such that y = g^x to a base g.

Anna picks a random value v from a set of values Z, and computes t = g^v and sends t to Carl.

Carl picks a random value c from the set Z and sends it to Anna.

Anna computes r = v-c*x and returns r to Carl.

Carl checks if t= g^r * y^c holds or not ( since r= v-c*x, y= g^x and by simple substitution, g^(v-c*x)* g ^ c*x = g^v = t).

Carl doesn’t know the value of x, by merely checking if t = g^r * y^c he can verify that Anna does indeed know the value of x.

Now while the above interaction is zero-knowledge, the problem with this is that Anna and Carl need to be online and exchanging values for it to work.

How can Anna prove to Carl that she has knowledge of something without Carl being online? She can do so by using a simple cryptographic hash function, as Fiat and Shamir theorized.

Let’s look how the example above would work in a non-interactive way:

Anna wants to prove to Carl that she knows a value x such that y = g^x to a base g.

Anna picks a random value v from a set of values Z, and computes t = g^v.

Anna computes c = H(g,y,t) where H() is a hash function.

Anna computes r = v – c*x.

Carl or anyone can then check if t = g^r * y^c.

So, as you can see, zero knowledge proofs were made noninteractive. And this was what laid the foundations for Zk-Snarks.

What is the use of Zk-Snarks?

Zk-Snarks stands for “Zero-Knowledge Succinct Non-Interactive Argument of Knowledge”. Its use in modern blockchain technology is immense. To understand its application, it is important to know how a smart contract works. A smart contract is basically an escrow of funds which gets activated once a particular function is done.

Eg. Anna puts 100 ETH in a smart contract that she gets into with Carl. Carl has to do a particular task, on the completion of which, Carl will get the 100 ETH from the smart contract.

This gets complicated when the tasks that Carl has to do are multi layered and confidential. Suppose you have entered a smart contract with Anna. Now, you will only get the payment if you do A, B and C. What if you don’t want to reveal the details of A, B, and C because they are confidential to your company and you don’t want any competitors to know what you have to do?

What Zk-Snarks does is that it proves that those steps have been taken in the smart contract without revealing what those steps actually are. It is very useful is protecting you and your company’s privacy. It can just reveal part of the process without showing the whole process itself and prove that you are being honest about your claims.

How do ZkSnarks work?

A Zk-Snark consists of 3 algorithms: G, P and V.

G is a key generator takes an input “lambda” (which must be kept confidential and shouldn’t be revealed under any circumstances) and a program C. It then proceeds to generate two publicly available keys, a proving key pk, and a verification key vk. These keys are both public and available to any of the concerned parties.

P is the prover who is going to use 3 items as input. The proving key pk, the random input x, which is publicly available, and the private statement that they want to prove the knowledge of without revealing what it actually is. Let’s call that private statement “w”. The P algorithm generates a proof prf such that: prf = P(pk, x,w).

The verifier algorithm V has basically returned a boolean variable. A Boolean variable has only two choices, it can be TRUE or it can be FALSE. So, the verifier takes in the verifying key, public input x and proof prf as input such as:

V(vk,x,prf)

..and returns TRUE if the prover is correct and false otherwise.

Now, about the parameter lambda. The value of the “Lambda” must be kept confidential because then anyone can use it to generate fake proofs. These fake proofs will return a value of TRUE regardless of whether the prover actually has knowledge of private statement “w” or not.

Functionality of ZkSnarks

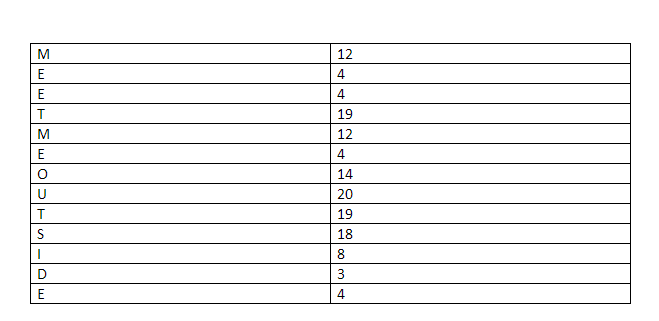
For showing the functionality of a Zk-Snark we are going to use the same example function that Christian Lundkvist used in his article for Consensys. This is what the example program looks like:

function C(x, w)

{

return ( sha256(w) == x );

}

Basically, the function C takes in 2 values as input, a public hash value “x” and the secret statement that needs to be verified “w”. If the SHA-256 hash value of w equals “x” then the function returns TRUE otherwise it returns FALSE. (SHA-256 is the hash function that is used in Bitcoin).

Let’s bring back our old friends Anna and Carl for this example. Anna being the prover and Carl the skeptic is the verifier.

The first thing that Carl, as the verifier, has to do is to generate the proving and verifying key using the generator G. For this, Carl needs to generate the random value “lambda”. As stated above, however, he needs to be super careful with Lambda because he can’t let Anna know its value to stop her from creating fake proofs.

Anyway, this is what that will look like:

G(C, lambda) = (pk , vk).

Now that the two keys are generated, Anna needs to prove the validity of the statement by generating the proof. She is going to generate the proof using the proving algorithm P. She is going to prove that she knows the secret value “w” which hashes (on parsing through SHA-256) to give the output x. So, the proving algorithm for proof generation looks like this:

prf = P( pk, x, w).

Now that she has generated the proof “prf”, she is going to give the value to Carl who is finally going to run the verification algorithm of Zk-Snarks.

This is what that will look like:

V( vk, x, prf).

Here, vk is the verifying key and x is the known hash value and prf is the proof that he has gotten from Anna. If this algorithm returns TRUE then this means that Anna was honest and she indeed had the secret value “w”. If it returns FALSE then this means that Anna was lying about knowing what “w” is.

The use of ZkSnarks in cryptocurrency

Save

Image Courtesy: Zcash

Zcash is a cryptocurrency launched by Zerocoin Electic Coin Company on 9th September 2016 and is the first example a cryptocurrency marrying the concepts of blockchain technology with ZkSnarks. It aims to provide completely safe and shielded transaction spaces for its users without revealing details (such as their addresses) to anyone.

Ethereum wants to integrate ZkSnarks as it enters its Metropolis phase and the way that they are planning to do so is by creating an alliance with Zcash which will include the mutual exchange of value. The chief developer of Zcash, Zooko Wilcox, gave a presentation in DevCon2 in Shanghai which explored the future of such an alliance. According to him, there are 3 ways that Z-Cash and by extension, zk-snarks could be integrated with Ethereum.

First method is called Baby Zoe (Zoe = Zcash on Ethereum). It adds a zk-snark pre-compiler on Ethereum and makes a mini Zcash smart contract on Ethereum. The idea is to see whether the Ethereum system can create a zk-snark enabled DAPP on top of its blockchain.

The Second method is to integrate the Ethereum computability inside the Zcash blockchain. As Wilcox puts is, the greatest asset of Ethereum is its computability and people want to see whether they can integrate it on a zk-snark based blockchain like Zcash. Can people create DAPPS on a blockchain made on zero knowledge proofs? That is something that they are waiting to see.

The third and the most exciting aspect is Project Alchemy. This is basically the connection and interoperation of the two blockchains such that one can seamlessly move between the two. The way that Zcash plans to do that is by cloning the BTC Relay. It is an Ethereum script which was written to create a Bitcoin light client inside Ethereum. The Zcash clone will use the same concept to create a Zcash light client inside Ethereum.

If this works then we will have the first, decentralized currency system in the world which facilitates the creation of DAPPS with zero knowledge ingrained in it.

Looking Ahead

There is no doubt that the introduction of zero knowledge proofs is going to be a huge game changer for Ethereum. In an increasingly open, connected and supervised world, any sort of privacy is welcome. How the integration happens remains to be seen, but going by the theoretical concepts itself, one can’t help but get excited.

What is Cryptoeconomics? The Ultimate Beginners Guide

What is cryptoeconomics? Ethereum developer Vlad Zamfir says that cryptoeconomics is:

“A formal discipline that studies protocols that govern the production, distribution, and consumption of goods and services in a decentralized digital economy. Cryptoeconomics is a practical science that focuses on the design and characterization of these protocols.”

Save

The blockchain technology runs on the principles of cryptoeconomics.

Let’s break it down. Cryptoeconomics comes from two words: Cryptography and Economics. People tend to forget the “economics” part of this equation and that is the part that gives the blockchain its unique capabilities. The blockchain wasn’t the first time that a decentralized peer-to-peer system was used, torrent sites have used it for ages to share files. However, in every sense of the word, it has been a failure.

Why was peer-to-peer file sharing a failure?

In a torrent system, anyone can share their file with a decentralized network. The idea was that people would download them and keep seeding aka sharing the file with the network for others to download. The problem was that this worked on an honor system. If you were downloading a file, then you were expected to seed as well. The problem is that humans are not really the most honorable of creatures and without any economic incentives it made no sense for people to keep seeding a file which took up unnecessary space in their computers.

Satoshi Nakamoto and the blockchain technology

In October 2008, an unknown man/woman/group calling themselves Satoshi Nakomoto released a paper which would lay the foundation for bitcoin. This would shake the online community to its very foundations, for the first time we had a working model for something based in cryptoeconomics. The way it differed from earlier p2p decentralized systems, was that people now actually had an economic incentive to “follow the rules”. But more than that, the true genius of the blockchain technology lied in how it circumvented the Byzantine General’s Problem to create a perfect consensus system (more on that later).

Cryptoeconomic properties of Bitcoin

So what are the properties that a cryptocurrency like Bitcoin has as a result of cryptoeconomics?

Let’s go through them one by and one:

It is based on the blockchain technology where each block contains the hash of the previous block and forms a continuous chain.
Each block will include transactions.
The blocks will have a particular state which is subject to change according to transactions. Eg. if A has 50 bitcoins and wants to send 20 bitcoins to B. Then The new state should show that A has 30 bitcoins left and B has 20 new bitcoins.
The blockchain must be immutable. It should be possible to add new blocks but the old blocks can’t be tampered with.
Only valid transactions should be allowed.
The blockchain should be downloadable and anyone anywhere can easily access and check a particular transaction.
Transactions could be added quickly to the blockchain if a sufficiently high transaction fee is paid.

There are two pillars of cryptoeconomics as the name itself suggests:

Cryptography.
Economics.

Now let’s explore how these two lend the blockchain its unique characteristics.

Cryptography

Blockchain technology uses cryptographical functions for its operations. Let’s looks at some of the main functions that run the blockchain:

Hashing.
Signatures.
Proof of work.
Zero Knowledge Proofs.

Hashing

In simple terms, hashing means taking an input string of any length and giving out an output of a fixed length. Bitcoin uses SHA-256 to take in an input string of any length and giving an out hash of 256 bits. So what are the applications of hashing in cryptocurrency?

Cryptographic hash functions.
Data structures.
Mining.

Cryptographic hash functions:

A cryptographic hash function has the following properties:

Deterministic: An input A will always have the same output h(A) no matter how many times you parse it through the same hash function.

Quick Computation: A function should return a hash of an input as quickly as possible.

Pre-Image resistance: Given h(A) which is an output of a hash function, it should be infeasible to determine input A.

Collision resistance: Given two inputs A and B and their hash outputs h(A) and h(B) it should be infeasible for h(A) = h(B).

Small changes: in the input should drastically affect the output of the hash function.

Puzzle Friendly: For every hash output Y and an input x. It is infeasible to find a value k, which will result in h(k|x) = Y.

The cryptographic hash functions greatly help with security and mining in the blockchain.

Data Structures:

The two data structures that are important in understanding the blockchain are Linked Lists and Hash Pointers.

Linked Lists: Linked lists are blocks of data which are connected to one after another. This is an example of a linked list:

Save

Each block in the list is pointing to the other via a pointer.

Pointer: Pointers are variables which include the addresses of the other variables. So they are variables which are literally pointing towards the other variables.

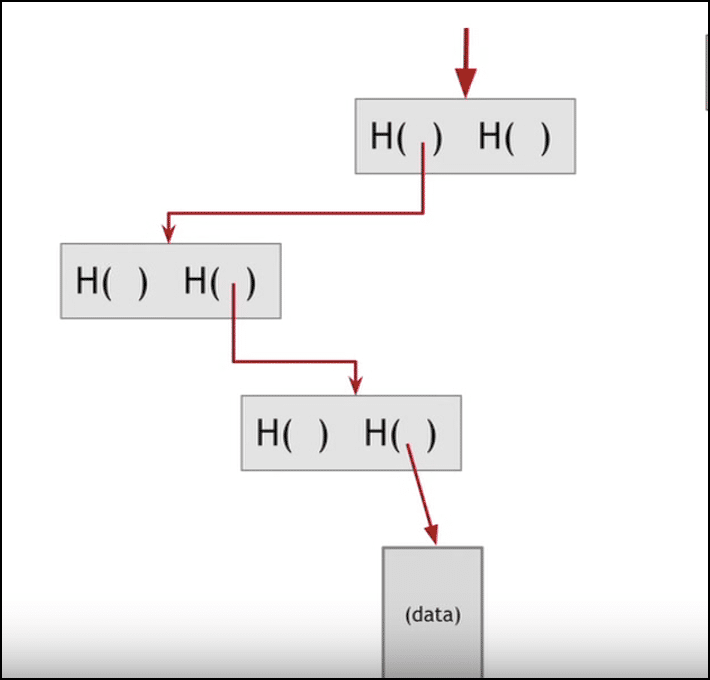
Hash Pointers: Hash pointers are basically pointers which not only has the address of other variables but also the hash of the data in that variable. So how does that help in the context of a blockchain?

This is what a blockchain looks like:

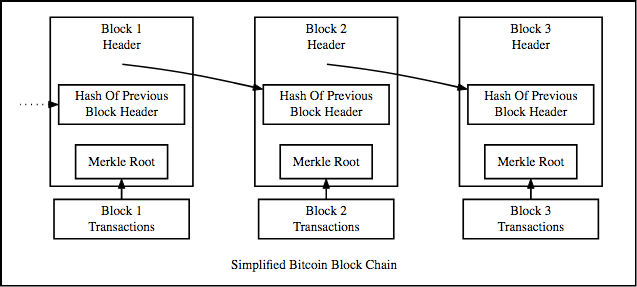
What is Cryptoeconomics- The Ultimate Beginners Guide

The blockchain is basically a linked list where each new block contains a hash pointer which points to the previous block and the hash of all the data in it. Just this one property leads into one of Blockchain’s greatest qualities….its immutability.

How are blockchains immutable?

Suppose in the diagram above someone tries to tamper with the data in block 1. Remember that one of the properties of cryptographic hash functions is that a slight change in the input data will greatly change the output hash.

So, even if someone tries to tamper with the data in block 1 even slightly, it will change its hash drastically which is stored in Block 2. This will, in turn, result in the change of the hash of Block 2 which will result in the change of hash in block 3 and that will keep ongoing on and on till the end of the blockchain. This will freeze up the chain, which is impossible, so just like that, the chain is rendered tamper-proof.

Each block also has its own Merkle Root. Now, as you are already aware, every block has a lot of transactions. If the transactions were to be stored in a linear manner, it will be extremely cumbersome to go through all the transactions just to find a particular one.

This is why we use a Merkle tree.

Save

In a Merkle Tree, all the individual transactions are distilled down into one root via hashing. And this makes traversal very easy. So, if someone were to access a particular data in a block, instead of going through them linearly they can simply traverse using the hashes in the Merkle tree to get to the data:

Save

Mining

Crypto-puzzles are used in order to mine new blocks and for that hashing is critical as well. So the way it works is that there is a difficulty level that is set. After that, a random string called “nonce” is appended to the hash of the new block and hashed again. After that is it checked whether it is less than the difficulty level or not. If it is then the new block is added to the chain and a reward is given to the miner(s) responsible. If it isn’t less than the difficulty, the miners keep changing the nonce and wait for a value which would be less than the difficulty.

As you can see, hashing is a critical part of blockchain and cryptoeconomics.

Signatures

One of the most important cryptographical tools that are used in cryptocurrency is the concept of signatures. What is a signature in real life and what are its properties? Imagine a paper that you have signed with your signature, what should a good signature do?

It should provide verification. The signature should be able to verify that it is you who actually signed the paper.
It should be non-forgeable. No one else should be able to forge and copy your signature.
Non-repudiation. If you have signed something with your signature, then you should not be able to take it back or claim that someone else has done it instead of you.

In the real world, however, no matter how intricate the signature, there are always chances of forgery, and you cannot really verify signatures using simple visual aids, it is very inefficient and non-reliable.

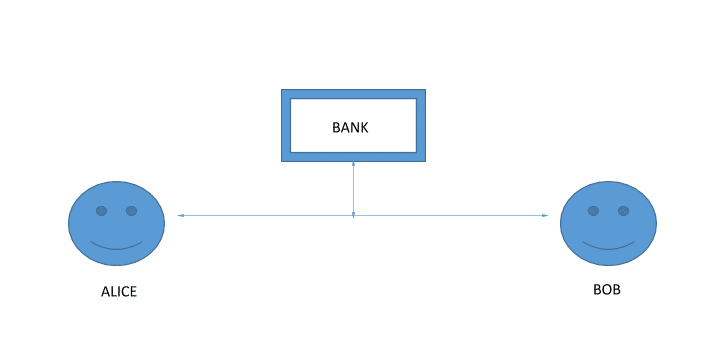
Cryptography gives us a solution using the concept of public and private key. Let’s see how the two keys work and how it fuels the cryptocurrency system. Suppose there are two people, Alan and Tyrone. Alan wants to send some very important data and Tyrone needs to authenticate that the data actually came from Alan. The way they are going to do it is by using Alan’s public and private key.

One important thing to note: It is infeasible to determine one’s public key from one’s private key. The public key is public as the name states, and anyone can have that key. The private key, however, is something that only you should have and you must NOT share it with anyone.

So, let’s go back to Alan and Tyrone if they are to exchange messages using the keys how will it look?

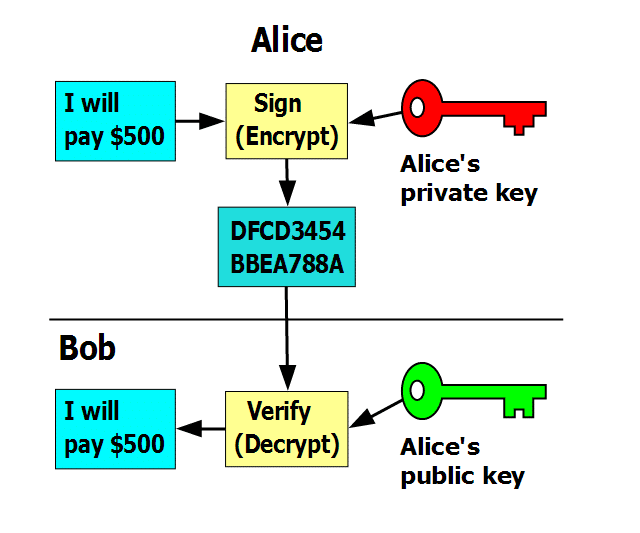
Suppose Alan wants to send a message “m”. Alan has a private key Ka- and a public key Ka+. So when he sends the message the Tyrone he will encrypt his message with his private key so the message becomes Ka-(m). When Tyrone receives the message he can retrieve the message by using Alan’s public key, Ka+(Ka-(m)) and retrieves the original message “m”.

To summarize:

Alan has a message “m” which he encrypts with his private key Ka- to get encrypted message Ka-(m).
Tyrone then uses Alan’s public key Ka+ to decrypt the encrypted message Ka+(Ka-(m)) to get the original message “m”.

Check out this diagram for a visual representation:

Save

Verification: If the encrypted message gets decrypted by using Alan’s public key then it verifies 100% beyond proof that Alan was the one who sent the message.

Non-Forgeable: If someone, say, Bob, intercepts the message and sends his own message with his private key, Alan’s public key won’t decrypt it. Alan’s public key can only decrypt messages encrypted with his private key.

Non-Repudiable: Similarly, if Alan says something like, “I didn’t send the message, Bob did” and Tyrone is able to decrypt the message using Alan’s public key, then this shows that Alan is lying. This way he can’t take back the message that he sent and put the blame on anyone else.

Applications in cryptocurrency: Now suppose Alan is sending some transaction “m” to Tyrone. He will first hash his transactions using a hash function. And then encrypt it using his private key. Tyrone knows that he is getting a transaction “m”, so he can then decrypt the message using Alan’s public key and compare the hashes of the of the resulting decryption with the hash of the transaction “m” that he has already. As hash functions are deterministic and will always give the same output to the same input, Tyrone can easily determine that Alan did indeed send that exact same transaction and there was no malpractice involved.

In simpler terms:

Alan has a transaction “m” and Tyrone knows that he is getting “m” as well.
Alan hashes m to get h(m).
Alan encrypts the hash with his private key to get Ka-(h(m)).
Alan sends the encrypted data to Tyrone,
Tyrone uses Alan’s public key to decrypt Ka+(Ka-(h(m))) to get the original hash h(m).
Tyrone can then hash the “m” that he originally had to get h(m).
If h(m) = h(m), as it should be because hash functions are deterministic, then this means that the transaction was free of malpractice.

Proof Of Work

When miners “mine” to form new blocks to add to the blockchain, the consensus system by which the blocks get approved and added is called “proof-of-work”. Miners use heavy duty computational power to solve cryptographical puzzles to satisfy a difficulty level. This is one of the most path-breaking mechanisms in blockchain technology. Earlier decentralized peer-to-peer digital currency systems used to fail because of something called the “Byzantine General’s Problem”. The proof-of-work consensus system finally provided a solution to this problem.

What is the Byzantine General’s Problem?

Save

Image Courtesy: Medium

Ok so imagine that there is a group of Byzantine generals and they want to attack a city. They are facing two very distinct problems:

The generals and their armies are very far apart so centralized authority is impossible, which makes coordinated attack very tough.
The city has a huge army and the only way that they can win is if they all attack at once.

In order to make successful coordination, the armies on the left of the castle send a messenger to the armies on the right of the castle with a message that says “ATTACK WEDNESDAY.” However, suppose the armies on the right are not prepared for the attack and say, “NO. ATTACK FRIDAY” and send back the messenger through the city back to the armies on the left. This is where we face a problem. A number of things can happen to the poor messenger. He could get captured, compromised, killed and replace with another messenger by the city. This would lead to the armies getting tampered information which may result in an uncoordinated attack and defeat.

This has clear references to blockchain as well. The chain is a huge network; how can you possibly trust them? If you were sending someone 4 Ether from your wallet, how would you know for sure that someone in the network isn’t going to tamper with it and change 4 to 40 Ether?

Satoshi Nakamoto was able to bypass the Byzantine General’s problem by inventing the proof of work protocol. This is how it works. Suppose the army on the left want to send a message called “ATTACK MONDAY” to the army on the right, they are going to follow certain steps.

Firstly, they will append a “nonce” to the original text. The nonce can be any random hexadecimal value.

After that, they hash the text appended with a nonce and see the result. Suppose, hypothetically speaking, the armies have decided to only share messages which, on hashing, gives a result which starts with 5 zeroes.

If the hash conditions are satisfied, they will send the messenger with the hash of the message. If not, then they will keep on changing the value of the nonce randomly until they get the desired result. This action is extremely tedious and time-consuming and takes a lot of computation power.

If the messenger does get caught by the city and the message is tampered with, according to hash function properties, the hash itself will get drastically changed. If the generals on the right side, see that the hashed message is not starting with the required amount of 0s then they can simply call off the attack.

However, there is a possible loophole.

No hash function is 100% collision-free. So what if the city gets the message, tampers with it and then accordingly change the nonce until they get the desired result which has the required number of 0s? This will be extremely time-consuming but it is still possible. To counter this, the generals are going to use strength in numbers.

Suppose, instead of just one general on the left sending messages to one general on the right, there are 3 generals on the left who have to send a message to the ones on the right. In order to do that, they can make their own message and then hash the cumulative message and then append a nonce to the resulting hash and hash it again. This time, they want a message which starts with six 0s.

Obviously, this is going to be extremely time-consuming, but this time, if the messenger does get caught by the city, the amount of time that they will take to tamper the cumulative message and then find the corresponding nonce for the hash will be infinitely more. It may even take years. So, eg. if instead of one messenger, the generals send multiple messengers, by the time the city is even halfway through the computation process they will get attacked and destroyed.

The generals on the right have it pretty easy. All they have to do is to append the message with the correct nonce that will be given to them, hash them, and see whether the hash matches or not. Hashing a string is very easy to do. That, in essence, is the process behind proof-of-work.

The process of finding the nonce for the appropriate hash target should be extremely difficult and time-consuming.
However, the process of checking the result to see if no malpractice has been committed should be very simple.

Zero Knowledge Proofs.

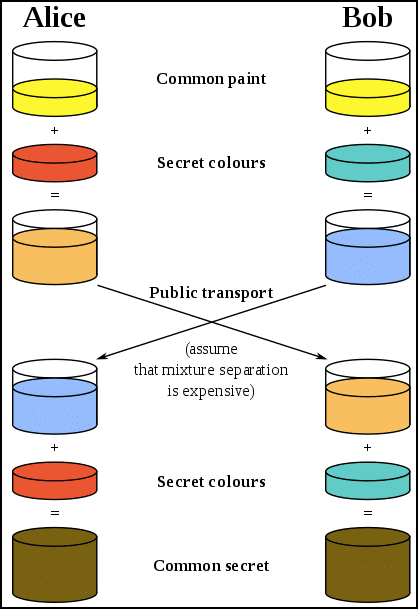
What is a zero knowledge proof (zkp)? ZKP basically means that a person A can prove to person B that they have knowledge of a certain piece of information without telling them what that knowledge specifically is. In this example, the person A is the prover and the person B is a verifier. In cryptography, this becomes especially useful because this helps in proving an extra layer of privacy for the prover.

For a ZKP to work it needs to satisfy certain parameters:

Completeness: If the statement is true then an honest verifier can be convinced of it by an honest prover.
Soundness: If the prover is is dishonest, they can’t convince the verifier of the soundness of the statement by lying.
Zero-Knowledge: If the statement is true, the verifier will have no idea what the statement actually is.

An example of a ZKP is the Alibaba cave, let’s see how it works. In this example, the prover (P) is saying to the verifier(V) that they know the password of the secret door at the back of the cave and they want to prove it to the verifier without actually telling them the password. So this is what it looks like:

Save

Image courtesy: Scott Twombly (YouTube channel)

In the diagram, as you can see, the prover does indeed appear in path B. But what if this was dumb luck? What if the prover didn’t know the passcode, and took the path B, was stuck at the door and by sheer fortune, the verifier told him to appear from path B, the one they were originally on anyway?

What is the application of ZKP in blockchain?

Many blockchain based technologies are using Zk-Snarks, in fact, even Ethereum in its Metropolis phase is planning to bring in Zk-Snarks and add it to its arsenal. Zk-Snarks stands for “Zero-Knowledge Succinct Non-Interactive Argument of Knowledge” and it proves a computational fact about the data without revealing the data itself.

They can be used to generate a proof of statement to verify each and every transaction by just taking a simple snapshot of each transaction which is enough to prove to the receiving side that a transaction was done without revealing the transaction itself.

This achieves two things:

The integrity and privacy of the transaction is maintained.
By not revealing the inner workings of the entire transaction the system maintain abstraction which makes it infinitely easier to use.

So these are some of the important cryptographical functions which are being used by the blockchain. Now let us look at the second pillar, Economics.

Economics

Like we mentioned in the beginning, the place where blockchain differs from other decentralized peer-to-peer system is that it gives its users financial and economic incentives to get some work done. Like with any solid economic system, there should be incentives and rewards for people to get work done, similarly, there should be a punishment system for miners who do not act ethically or do not do a good job. We will see how the blockchain incorporates all these basic economic fundamentals.

Must Read: Cryptocurrency Game Theory

There are two sets of incentives that participants in the blockchain have:

Incentive Set #1

Tokens: The actors who actively participate and contribute to the blockchain get assigned cryptocurrencies for their efforts.
Privileges: Actors get the decision-making rights which gives them the right to charge rent. Eg. Miners who mine a new block become the temporary dictator of the block and decide which transactions go in. They can charge transaction fees to include transactions within the block itself.

Incentive Set #2

Rewards: Good participants get a monetary reward or decision-making responsibility for doing well.
Punishments: Bad participants have to pay a monetary fine or they have their rights taken away for behaving badly

How do cryptocurrencies have value?

Cryptocurrencies have value because of the same reason that money, in general, has value, trust. When people trust a commodity and give it value, it becomes a currency, that’s the same reason why fiat has value and why gold had value in the first place. So when a given commodity is given value, the value changes in accordance with one of the oldest rules in economics, called Supply and Demand.

What is Supply and Demand?

Save

This is the supply-demand graph and one of the most common things that you will see as in economics. As you can see, the demand for the commodity is in an inverse proportion with its supply. The spot where the two graphs meet is the equilibrium i.e. the sweet spot where you want to be. So, let’s use this logic for cryptocurrency and, in general, bitcoin.

The supply of bitcoins is fixed at 21 million. That’s the market cap on all bitcoins. Since the total number is fixed there are several things that need to be considered when it comes to the supply of bitcoin. Because of this, certain regulations need to be made to make sure that bitcoins become progressively harder to mine. If these steps are not taken, the miners will mine indiscriminately, pumping out the remaining bitcoins and putting it in the market, decreasing its overall worth.

In order to make sure that miners don’t pump out all the bitcoins at once the following steps are taken:

A new block is added to the chain only at the interval of 10 mins which leads to a reward of 25 bitcoins. The time has to be fixed to make sure that miners don’t just keep adding blocks to the chain with no regulations.

The second thing that the bitcoin protocol does is that it constantly increases the difficulty level. As explained above, during the mining process the hash of the block along with the nonce needs to be less than a particular number. This number is called the “difficulty level” and usually begins with a number of zeroes. As the difficulty increases the number of zeroes increases as well.

With these two factors and the fact that mining has become a lot more specialized process which includes humongous investment, the entire process makes sure that the supply of bitcoins in the market is kept at check. And this is true for all cryptocurrencies, using proof of work, as well.

The Demand of the cryptocurrency depends on a lot of factors:

What is the history of the currency?
Has it been subject to a hack lately?
Does it consistently generate results?
How good is the team behind it?
Does it have potential to become better?
How much is the hype around it?

All these factors determine how “hot” the currency is and as a result, the value shifts depending on its demand.

The Game theory in blockchain

So how does an unregulated, decentralized peer to peer system remain honest? Miners have a lot of power and they can easily commit crimes and get away with it. This is where all the previous attempts at a decentralized system failed, users are humans and humans are prone to “bad” behavior. So how do you keep a decentralized system of humans honest? The answer lies in one of the most fundamental economic ideas: Game Theory.

Game theory is basically the study of strategic decision-making. Making decisions which make the most sense to you, keeping in mind the decision of the competitors is basically what game theory is all about. One of the most fundamental concepts of game theory is the “Nash Equilibrium”.

What is Nash Equilibrium?

A Nash Equilibrium is a state where a party takes the most optimal strategy keeping in mind the actions of the other party and they can’t gain anything by changing around their strategy. Let’s see an example of the Nash Equilibrium in action.

Now consider the above table that we call a “Payoff Matrix”. The numbers are units of payoffs that a person will get upon taking (or not taking an action). So let’s analyze:

If A Takes Action:

Then B has a payoff of 4 if it takes action and 0 payoff if it doesn’t take action. So the optimal strategy for B is to take action.

If A Doesn’t take Action:

Once again, B has 0 payoffs for not taking action and a payoff of 4 if it does take action.

So we can conclude that regardless of what A does, B’s best strategy lies in taking action. Now, similarly, let’s checkout the what is the best strategy for A.

If B takes Action:

A has a payoff of 0 for not taking action and a payoff of 4 for taking action. So the best way for A is to take action.

If B doesn’t take Action:

A has a payoff of 0 for not taking action and a payoff of 4 for taking action.

So, regardless of what B does, A’s the best way forward is to take action.

We can hence conclude that for both A and B the best way to go ahead is to take action.

Hence the Nash Equilibrium is:

When both of them take action.

Now, what is the application of the Nash Equilibrium in the blockchain? Well, it won’t be a stretch to say that the blockchain exists and the miners remain honest BECAUSE the chain itself is in a self-imposing Nash Equilibrium.

Let’s take an example:

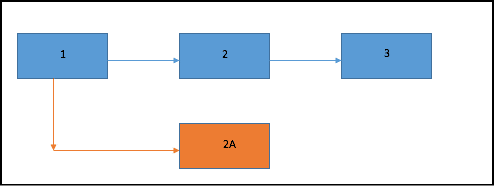
Consider the above blockchain. The blue blocks 1,2 and 3 are part of the main chain. Now suppose a malicious miner mines a block 2A and is attempting a hardfork for his own financial gains. What is stopping the other miners from joining him and mining on the new block?

Well, the miners have a very hard and fast rule, any block that is mined on an invalid block is not considered a valid block. So, the other miners will simply ignore the invalid block and keep mining on the old chain anyway. Remember, all currency works on trust and perceived value, so the currency that the malicious miner may mine from the new block will not be considered of any value at all. And remember, mining is a very expensive process, so why will anyone waste so much resource on a block that may or may not even be considered valid?

Now you may be thinking, what if a lot of miners decide to join the new miner and mine on the new block? The problem with that is that the blockchain network is a huge and widely distributed network wherein communication and coordination is next to impossible. Keeping that in mind, a coordinated attack like that on the blockchain is infeasible. Most miners will simply choose the route where they get a maximum payoff, and this way the Nash Equilibrium of the main chain is maintained.

Punishment in the blockchain

Like with any efficient economic systems, good actions should be rewarded and negative actions should be punished. How does punishment work in a game theory model? Imagine a payoff matrix where the payoff for the participants is high but the implication on the society, in general, is very high. Eg.

Suppose there are two people A and B and they are both about to commit a crime. Now according to the matrix, the payoff for both of them is high when they commit a crime so their Nash Equilibrium lies in both committing a crime. Now while this does make sense logically, the implications on the society, in general, is very bad. Humans, more of than not, are motivated by personal greed and not everyone is altruistic. If this were to hold true, the world will be a terrible place to live in. So, how did humans counteract this? By introducing the concept of punishment.

Suppose we have a system where for every -0.5 of utility taken for them public, there will be a punishment factor of -5 on everyone who commits a crime. So, let’s add the punishment factor on the payoff matrix above and see how that changes the table:

As you can see above, the payoffs change drastically and the Nash Equilibrium changes to (1,1), as in both don’t commit a crime. Now, punishment is expensive, a utility of -0.5 is taken from the society after all. So what is the incentive for society to join the punishment game? The way this question was answered was by making punishment mandatory for everyone i.e. anyone who is not participating in the punishment game is punished as well. An example of this is a tax-driven police force. The police can punish the perpetrators but a utility in the form of tax is taken from the public. Anyone who doesn’t pay the tax and participate in the game is considered a criminal themselves and punished accordingly.

In a blockchain, any miners who are not following the rules and mining illegal blocks are punished by having their privileges taken away and risk social ostracization. The punishment becomes even more severe when proof-of-stake is involved (more on this later). By using simple game theory and punishment system, the miners are kept honest.

More incentives for miners

When a miner(s) successfully mines a block, they become the temporary dictator of that block. It is completely their jurisdiction as to which transactions go in the block and the speed of the said transactions. For the transactions to be included, they can charge a transaction fee. This incentivizes the miners because they get additional financial rewards OVER the reward they gain from mining a new block anyway (25 BTC in bitcoin and 5 Eth in Ethereum).

In order to make the system fair and to make sure that not the same miners get to mine new blocks and collect the rewards every single time, the mining difficulty level is adjusted periodically. This makes sure that the miners who get to mine a new block is completely random. Over the long run, mining is a zero sum gain, in other words, the profits that a miner gets from mining a new block eventually gets adjusted because of the costs of mining.

P+Epsilon Attack

A proof of work system, however, is vulnerable to a particular type of attack called the “P+ epsilon attack”. In order to understand how this attack works we must define some terms beforehand.

Un-Coordinated Choice Model: An uncoordinated choice model is a model where all the participants don’t have the incentive to work with one another. The participants may form groups but at no time is the group big enough to become a majority.

Coordinated choice model: This is a model where all the participants coordinate because of a common incentive.

Now it is assumed that the blockchain is an uncoordinated model, but what if there is an incentive for the miners to do an action which goes against the integrity of the blockchain? What if there is a bribe involved to make the miners take a particular action? This is where the bribing attacker model comes in.

What is the bribing attacker model?

Imagine an uncoordinated model. Now, what if an attacker enters the system and incentivizes the miners to coordinate with each other after giving them a bribe? This new model is called a bribing attacker model. In order to successfully bribe the system, the attacker must have two resources:

Budget: The total amount of money that the attacker has that they are willing to pay to make the miners take a particular action.
Cost: The price that the miner actually ends up paying.

However, if an attacker does decide to attack the blockchain, we arrive in an interesting conundrum… and this is where the “p + epsilon attack” comes in. For reference check out this table:

Image courtesy: Vitalik Buterin Presentation.

Imagine a simple game such as an election. If the people vote for a particular person if they vote the same way everyone is voting, then they get a payoff but otherwise, they don’t. Now imagine, that a briber enters the system and lays down this condition to an individual. If you vote AND the others don’t vote, then you will get a payoff of “P + ε”. The usual payoff AND an extra bribe of ε on top of that.

So now, the payoff matrix looks like this:

Image courtesy: Vitalik Buterin Presentation.

Now imagine this scenario, everyone involved in this game gets to know that if they vote anyway, then there is a chance that they may get a payoff, but if they don’t vote then there is a 50-50 chance of them getting a payoff.

What do you think the players will do then? Of course, they are going to vote to get a guaranteed payoff. Now, this is where things get interesting. As can be seen in the matrix, the briber only has to pay the bribe “ε” when only person votes while the others don’t. However, in this situation, since everyone is voting, the Nash equilibrium shifts to:

That’s right, the briber didn’t even need to pay the bribe!

So, let’s approach this problem from the POV of the briber:

Convince the group to vote a particular way.
Achieve the goal without even having to pay the bribe.

It is a huge win-win scenario for the briber and this has heavy implication on the blockchain especially in a proof-of-work system. Let’s check out our old hypothetical blockchain again:

Suppose the briber really wants the chain to hardfork and declares that a group of miner who opts to join the new chain will get a bribe of ε, this will incentivize the entire miner community to coordinate and join the new chain. Obviously the bribe has to be extremely high for something like this to happen, but as we have seen in the briber attacker model above, the attacker won’t even need to pay the said amount. According to Vitalik Buterin, this is one of the biggest problems of the proof of work system, its vulnerability to the P + epsilon attack.

The solution lies in proof of stake.

The solution to this form of incentive driven attack lies in proof of stake. In this system, the miners have to put up a portion of their personal fortune and invest it in future blocks. As an economic system, this is much better because the punishment in it is way more severe. Instead of having their rights taken and getting away with a “tap to their knuckles”, miners now face the very real possibility of their stake and fortune being taken away.

So, how does this help in preventing P + epsilon attacks? Put yourselves in a miner’s shoes. You have a part of your fortune invested inside a block which is to be added in the main chain. Now a briber comes and tells you that you can get an extra payoff if you make your block join the main chain. BUT, if the chain doesn’t get approved then there is a huge risk of you losing all the money that you have invested in the block. Plus, as the P + Epsilon attack states, you won’t even get the extra payoff from the bribe. For a miner, once that they have invested a stake, it is a no brainer for them to continue in the main chain and not to get involved in any malicious activities.

Conclusion

So as you can see, cryptography and economics have combined in a very beautiful and intricate manner to create the blockchain technology. The growth that it has experienced over the last few years is staggering and it is only going to get better and more widely used.

ICO Basics, To Invest or Not? Cutting Through The Bullshit

ICO Basics, To Invest or Not? Cutting Through The Bullshit. There are many terms associated with the cryptocurrency world that has become, more or less, very mainstream over the last 4-5 years. Everyone has an idea about what a “blockchain” is and people definitely know what a “bitcoin” is.

Lately, however, one term has been gaining more and more mainstream attention. That term is “ICO” or Initial Coin Offerings and has raised OVER $1.3 Billion for blockchain based start ups. It has been called everything from “revolutionary” to “a Ponzi scheme. Before we get into the meat of this, we need to understand everything that surrounds this astounding phenomenon.

The origins of ICO

Save

In the real world, companies can always secure funds by approaching angel investors and venture capitalists but by doing that, they would have to give away a share of their equity to them. What companies wanted, was to get a lot of funds without giving away equity and ownership. The only way that they could do that was by going public.

The way companies do this is by holding an IPO aka Initial Public Offering. How does an IPO work?

In an IPO a private company basically decides to put up its private shares up for sale to the general public. Anyone anywhere can buy the shares of the company. Initially, these shares are dirt cheap and if the company hits it big then there is a chance of your shares ballooning up to exorbitant prices. We have all heard stories of the masseuse who became a multi-millionaire after her 500 “useless” stocks in Google matured over time.

So, people started wondering what would happen if we used the same concept and put it on a blockchain based environment. This is what gave birth to the concept of ICOs. ICOs are pretty similar to IPOs but with 3 major differences.

Firstly, the ICO was decentralized with no central authority, secondly, the ICOs lacked the tedious red tape that most IPOs were bogged down by and finally, they were unregulated while IPOs have always under been heavy regulation. Now there was a problem that blockchain based companies were facing when it came to ICOs. In an IPO, the investors got shares in return of their investment. What would a blockchain based company give away in exchange of capital? They had to invent the blockchain equivalent of a share and that was when they came up with the idea of “Tokens”.

What is a Token?

An ICO is a sort of mixture of an IPO and a crowd-sale. When you are interested in a particular project in the blockchain, the way you can gain access to it is by sending the developing team some amount of money, which is usually paid in Bitcoin or Ethereum and getting the equivalent amount of tokens in return.

Tokens have gained even more prominence since the advent of Ethereum. Ethereum provides a platform where you can use the blockchain technology not just for making currency, but to make decentralized applications (DAPPS) as well. If you want to use these DAPPS then you will need the tokens that are native to its respective environment. There are two categories that all tokens fall under:

Usage Tokens.
Work Tokens.

Usage Tokens: These are tokens that act as native currency in their particular environment and can be exchanged for other tokens or FIAT money. Ether is a great example of a usage token. In short, usage token is a currency.

Work Token: Not all tokens, however, act as currency. Some tokens are there to give you various rights within their native environment. Eg. If you were a DAO token holder, then you had the right to vote on whether a particular DAPP could get funding from the DAO or not.

How do you make a token?

Making a token is deceptively simple. By far the easiest method is to go on Token Factory and fill up the following fields:

ICO Basics, To Invest or Not? Cutting Through The Bullshit

Save

Firstly, you will have to determine the total supply. You don’t want a humongous amount of tokens available, that will kill their value.

Then you have the name field. Give your tokens any name you want. Make it sounds professional though if you want a good and profitable ICO.

Determine how many decimals places the value of your tokens will go to.

And finally, decide on a symbol for your token! It is that simple.

Now., if you are one of those DIY types who would prefer coding their tokens then that is a possibility as well. If you are making a DAPP in Ethereum you can simply use the solidity code to create your own token contract. This is what a simple token contract looks like:

Save

The block of code is divided into 3 parts:

The Mapping.
Giving the creator all the tokens.
Transfer the sender the requisite amount of tokens for the ether.

Now we will go into the code and understand what is exactly happening and how it is working. It may appear complicated on the surface but once you go deep into it, you will see how simple and easy to understand it is.

The Mapping:

Ethereum, like all cryptocurrency, is an open ledger. So it makes sense that all token made on an Ethereum contract will be registered on an open database clear for everyone to see. The mapping function makes sure of that.

The creator getting all the tokens:

When all the tokens are created, the entire supply goes to the contract creator who can then send the tokens to anyone who funds the project with ETH.

The Transfer:

The last part of the code is the transfer.

You will give your tokens an initial value and based on the amount of ETH that you are getting paid by the sender, they will get the requisite amount of tokens. The same number of tokens will cut from your balance and it will be added to the sender’s balance.

As you may have already guessed, there are thousands of tokens out there, and while that’s a good thing, there is also a major flaw that needed to be addressed. Think about this, if everyone designed their own tokens giving it their own unique twist, it will be an absolute horror show to save them in a wallet. Many times you will have to follow elaborate and needlessly complicated steps just to store your tokens in a wallet. That would have been a nightmare. What was needed was a standard or a basic blueprint for all tokens to follow. Fabian Vogelstellar, one of the founders of the Mist Wallet came up with the solution with his ERC20 token standards.

What is the ERC20 Token Standard?

The ERC20 standards have been put in place so that all Ethereum tokens follow a particular rule and standard. While this is not an enforced rule, most DAPP developers are encouraged to follow the standards to ensure that their tokens can undergo interactions with various wallets, exchanges and smart contracts without any issues.

These standards also helped others gain an idea of how future tokens are expected to behave. ERC20 tokens have gotten widespread approval and most of the DAPPS sold on ICO’s have tokens based on the ERC20 standard. So what are these standards?

They are basically a set of 6 functions which, when executed, do the following 4 activities:

Get the total token supply.
Get the account balance.
Transfer the token from one account to another.
Approve the use of the token as a monetary asset.

How does an ICO work?

So now that you have gotten a crash course on what tokens are and how they work, let’s do a deep dive on ICOs and why, for better or for worse, people are calling it the new “Gold Rush”. A number of millionaires that ICOs have made in the last year or so is staggering. Check out this graph:

Check out this graph:

Save

Over the past 12 months, have raised over $600 million as opposed to $140.30 million by established Venture Capitals. That is mind-boggling! So what is it about ICOs that has attracted so many investors? ICO is the rockstar of the investment world, it is the untamed wild genius wearing a torn t-shirt and baggy jeans, living among a group of suit-wearing snooty businessmen. There is something extremely seductive about the concept.

Think about this, anyone, with an idea for a project, can gain massive financial backing from a community without being bogged down by politics or endless red tape. The idea that anyone anywhere can get the financial backing they need in an unregulated manner was a welcome idea for all. No longer will investments be reserved just for the uber-rich, anyone can gain the funds to make their dreams a reality.

The exact procedure behind an ICO can be broken down into the following steps.

Firstly, the developers will announce their intention of making the project to generate hype and interest in the project. This step is very important because first impressions are everything.

Then, the developers will create a white paper. A white paper is a document issued by the developers which highlight their project and the specific features of that project that makes it enticing for the potential investors. While it is true that white papers are supposed to be a sales and marketing tool, it is nowhere near as flashy and over-the-top as a brochure or a sales letter. Whitepapers are written in an academic manner and the specific purpose is to entice the investors by showing its potential and features. They are at least 2500 words long and are meant to be purely informational.

After that, they will run the white paper through prominent members in the blockchain community to get their backing. Getting this backing is critical because this is where they will gain the credibility required to carry forward with the project.

Now, they will need to create the tokens which they are going to exchange for Bitcoin or ETH in the token sale. The process of token creation has already been covered above. Developers will have to decide the limit to the number of tokens and the amount that they want to charge for each token. Usually, the price of these tokens is very low at the start of the ICO. Setting a cap on the number of tokens is necessary because having a limited supply of tokens automatically increases their demand (according to the law of supply and demand).

Along with the cap on the number of tokens issued, developers will have to decide a time at which they want to hold their ICO. Selecting the time, and the amount of time it runs for is CRITICAL and this will be covered in detail later on. Along with that they also need to decide on the cap for the amount of money they will be taking in.

Once all these are decided, the developers choose a platform where they can advertise their ICO. Earlier it used to be tough to do so because developers had to convince people to come to their websites to gain more information about the ICO. But now, there are a number of websites which provide the platform for developers to address this particular need. Some of the best ones are:

Waves.
ICONOMI.
State of DAPPS (for Ethereum Tokens only).
TokenMarket.

Think of these websites as Kickstarter or Indiegogo of the crypto world. Once the ICO has been advertised the developers can then actually do the ICO.

For a visual representation of how an ICO works:

Save

Investors send the coins to the public address of the developers and in exchange, they get tokens in return.

So to summarize:

Firstly, the developers declare their intention of making the project.
Then, the project developers create a white paper which includes the details of their project explained in a descriptive way.
They get the backing and confidence from certain prominent members in the cryptocurrency world who act as “advisors”.
They then create the tokens and decide on various caps such as a token cap, money cap, and time cap.
Advertise the ICO using one of the platforms mentioned above.
Hold the ICO.

In the broad spectrum of things there are two different kinds of ICOs:

Currency ICO.
Project ICO

Currency ICO

A currency ICO is when developers bring in a new currency system. The developers give out tokens which become new cryptocurrencies in exchange of the older more established coins such as Bitcoin and Ethereum. The reason why people are drawn to these ICOs are that of investment opportunities. One of the best examples of these kinds of ICOs is the Ethereum ICO.

In later 2013, a young programmer named Vitalik Buterin was working for Bitcoin as a developer and was getting increasingly frustrated. He realized that the blockchain technology had more potential than being a mere currency system. His vision was to make an alternate form of the internet. This vision was Ethereum, a platform where people not only will have access to a new form of currency (Ether) but they will also be able to create and develop a newer form of DAPPS on the platform itself.

The Ethereum ICO lasted for 42 days and went on from July-August 2014 and raised >$18 million. Back then it was the biggest crowdfunding even in human history. The early birds got a humongous ROI. In the beginning, if you invested just 1 BTC you would get 2000 ether in return. The current valuation of those 2000 ether is ~$420,000. Not bad for a $2500 investment! But more than the ROI the biggest thing that makes this particular ICO so important in crypto history is the concept of the project itself.

If you want an advertisement for why ICOs are so important, just read up on the Ethereum ICO. This was one man with a vision who got a dedicated and talented team around him, got the white paper out, convinced people to invest in his project and then ultimately made one of the most important platforms in crypto history. This is what ICOs should be like.

Project ICO

Along with the currency ICO we have the project ICOs which issue “work tokens”. When you buy these tokens in the crowd sale you gain certain rights and votes inside the environment of the DAPP itself. One of the most famous, and consequently, infamous examples of this kind of ICO is the DAO.

The DAO aka the decentralized autonomous organization was a decentralized venture capital fund which was going to be used to fund future projects made in the Ethereum eco-system. This how it was supposed to work. People invest money in the DAO by giving ether and they get “DAO Tokens” in return. These DAO tokens made the holders part of the DAO community. So, suppose Jill wanted a project to be funded by the DAO, she would introduce the project to the DAO community. The token holders will then hold a vote and if Jill gets the majority vote then she would gain the required funding from the DAO itself.

This was a revolutionary idea and was getting mainstream press exposure as well. The ICO went down in history as one of the biggest ever. The ICO raised $150 million in ether, that was the 14% of the total ether issued at that time and everything was looking up. Unfortunately, that is when the infamous DAO Attack happened and a total of $50 million worth of ether was taken away. This attack had huge repercussions because this was what caused the Ethereum hardfork and resulted in two different Ethereums: Ethereum and Ethereum Classic.

Another great example of the “Project ICO” is Augur, a decentralized market prediction system.

ICOs nowadays are raising a ridiculous amount of money, the Brave ICO, an Ethereum based browser raised in $35 million in 30 seconds. That’s ~$1.2 million per second!! The Tezos ICO recently became one of the largest ICOs of all time by raising more than $200 million. SO the question that you are probably thinking of right now is,
“How do you make sure that the funds that you are investing is going to be used properly by the developers?” What if they just run away with it? Let’s answer that question.

What steps should be taken to ensure the safety of the funds aka how to not get scammed?

Unfortunately, because of the unregulated nature of the ICOs and the sheer amount of money to be made in this space, it does attract a lot of scammers. If you are investing in an ICO then you would want some assurances on your end that all the funds that you are going to invest are going to be used in a right way. So what should you be looking into when you are about to invest to make sure that you are not going to get scammed?

The project developers should be able to clearly define the purpose of their project using simple and short sentences. If they are taking too much time and beating around the bush, then that either means: their agenda is not clear or they are hiding something. Both of which are not that encouraging scenarios.

Make sure that the developers are not anonymous. There should be 100% transparency when it comes to their names, business plans, locations etc. You should be able to contact them regarding any and all information that you need to get from them.

There should be a legal framework between the developers and the contributors including terms and conditions set for the ICO.

Lastly, and most importantly, you need to make sure that the ICO funds are being stored in an escrow wallet. An escrow wallet is basically a multi-sig wallet which needs multiple keys to be opened. One of those keys must be held by a neutral third party.

If you keep these 4 points in mind, then you will be able to spot the scammers with relative ease and invest in projects which have real potential.

So are we in an ICO bubble right now and is it going to pop?

With the sheer amount of money going into ICOs nowadays and everyone and their mothers wanting a piece of that ICO pie, there are legit fears going around of ICO being a bubble much like the dot com bubble and the real estate bubble. To understand how a bubble works, let’s look at one of the most famous examples of the bubble, the dot-com bubble which went from 1997-2002.

Around 1997, the internet became big and tech companies began to emerge everywhere. Investors started putting in their money and flipping their investments into huge sums. Eventually, everyone who saw this started getting major FOMO (fear of missing out) and they began giving away their money to companies without even having any idea as to whether the business had the potential to work or not. Common sense went out of the window and every random internet business was making a killing in the IPOs. Warren Buffet noted that:

“The fact is that a bubble market has allowed the creation of bubble companies, entities designed more with an eye to making money off investors rather than for them. Too often, an IPO, not profits, was the primary goal of a company’s promoters.”.

BOOM! He hit the nail right on the head, most of the companies that got millions from their investors failed and some turned out to be nothing more than scams. Eventually, the bubble burst in 2002.

Companies crashed and lost millions within a year. One of the most infamous examples of this is Pets.Com which lost $300 million in just 268 days! However, while 1 in 2 companies got shut down, the companies that did survive, hung on and changed the way we live today. One of the best examples of that is Amazon. Before the bubble burst, Amazon stocks were at $100/share. After the burst, it went down to $7/share but eventually, it went up to $600/share.

The parallels between the ICO bubble and the dot-com bubble are a bit frightening and as they say “if you don’t learn from history, it is going to repeat itself.” Much like dot-coms, the ICOs have attracted a lot of investors who don’t want to miss out on the gold rush. Much like the dot-coms ALL the investing is done purely from speculation. You have to realize that most of the companies that you are investing in, in ICOs barely have anything ready. Most of them don’t have the alpha version of their end result, it is all based on speculation and the potential of the project.

As with anything, most of these projects will fail to get the end results. The reason why the Ethereum ICO worked so wonderfully was that it had a dedicated and driven team of talented developers who were a day in and day out to make it a success, same with Golem. Another problem plaguing the ICO is the greed of the developers. Some developers are making projects ONLY so that it can look enticing enough for a good ICO. They have no interest in carrying through nor do they have any inclination of turning a profit for their investors.

The parallels are very apparent and it can get real scary thinking about it. But we are not market experts. All we can do is speculate. We don’t know whether we are living in the “ICO bubble” or not, nor do we know whether it is a bubble that is going to pop. What we can tell you to do is to be smart with your money. Don’t get enticed by shiny objects, and have basic common sense. Read the points we have given above to know whether an ICO is a scam or not.

So if I am a developer how should I approach ICOs?

If you are a developer, then first and foremost have a very clear idea and agenda as to what your project is and what do you want to do with it. You must state the purpose of your project and the future that you envision with it. You must also choose the platform that you want to advertise your ICO in (waves, iconomi etc.) and then you must design your tokens.

After you are done creating your white paper and running it through the advisors and getting legal backing, the most important thing that you need to do is to pick a good time and date. Nothing kills an ICO faster than not getting the timing right. So when selecting the time of the ICO to keep the following points in mind:

Do not choose holiday weeks or weeks when important people take off: You need as much hype as possible and the best investors for your ICO. Do not hold your ICO during spring break when most people, including reporters, take off. Similarly, if there is an important event around the week then it’s best to not have your ICO during that time. As Margaux Avedisian says, if your main investors are going to be in The Burning Man, then it is best to not have your ICO during that week,

Day of the week: You must notify the working patterns of your target investors and see which day best suits them. It is best to not choose a weekend for your ICO.

Time Cap: While there are some ICOs that meet their target in 10 mins or even 35 seconds, those are the rarest of the rare scenarios. Even the Ethereum ICO took 42 days, even though that was before ICOs became so popular. So you have to decide on the time cap and the amount of time that you are willing to run your ICO for.

Time Zone: If your target investors are Americans and then it makes little to no sense to have your ICO during midnight EST. Decide where you want your target investors to be from and decide on a time that will be convenient for them.

We cannot overstate the importance of time for your ICOs, the initial period is critical because that will determine how well your ICO will go. If you are a developer, then you will need to decide on the time after doing quite a bit of research. It is worth it in the end.

What are the Pros and Cons of ICOs?

Pros of ICO

Gives opportunities to promising projects: Think of what Ethereum has accomplished in the last year. From becoming the second most powerful cryptocurrency in the world to providing a platform for DAPP creators to create their projects. It is truly becoming the “platform where the future will be built”. All this got started because of an ICO.

Doesn’t require unnecessary paperwork: Many projects don’t get executed because they get caught up in the red tape. For raising funds through IPOs or crowdfunding the project developers need to go through a lot of paperwork and more often than not, they just don’t get the documentation required to collect funds for their project. On the other hand, all that you need to do take part in an ICO is create a “white paper” (The white paper contains all the details of your project.) After that, anyone can read the white paper and choose to invest in the project if it interests them.

Community building: It gives the project creators an opportunity to build a community around their projects. Having a healthy community gives a product immense credibility. Plus, the members of the community can have real say in the direction of the projects and keep the creators accountable.

Exposure for projects: The hype that surrounds an ICO can do wonders for the exposure of the project. The more the exposure, the more the people will know about the project. This increases the number of potential investors.

Early access to potentially valuable tokens: Some tokens have the potential of becoming truly valuable cryptocurrencies. ICOs give investors an opportunity to invest in tokens, with potential, for dirt cheap. Eg. During the Ethereum presale, 1 Ether cost 35-40 cents. Right now, as of writing, 1 Ether costs ~$277.

The incentive for innovation: The roaring success of various ICOs over the last 12 months has given extra incentive to various developers to innovate and develop more exciting projects.

Cons of ICO

Attracts a lot of scammers: Because there is so little paperwork involved in ICOs it attracts many scammers who can simply create a bogus white paper and make off with a lot of money. Some developers also purposefully omit certain important details from their white paper to make their projects look more appealing than they actually are. The biggest consequence of all these scams is the decreased faith of the public in blockchain technology which can potentially spell absolute disaster.

Based on pure speculation: When you are investing in a project in an ICO you are investing in the idea of the project. You read the white paper and if you think that the team is credible and the project has promise than you invest. So, basically, you have no idea whether the project will even be successful or not. Over 90% of the startups fail and blockchain projects are not immune to that as well. Plus, the developers may get lazy and not even bother to finish what they have started. And, let’s not forget, there is always the possibility of a project getting ruined because of hacks and attacks. The DAO is a perfect example of that.

Whaling: Let’s take the example of what happened in the, now infamous, BAT ICO. The ICO got over in just 24 seconds and they were able to raise 35 million USD! The shocking part was, not a lot of people were able to take part in the ICO at all as major chunks of the tokens were bought by certain individuals. In fact, a quarter of the BAT tokens are owned by one person!

Save

These people are called whales. Basically, people who have a lot of money and resources and they rig the ICO game in their favour. The way they do it is by paying extremely high mining fees which help them “cut in line” and get first preference during ICOs. In the case of the BAT ICO, whales paid as much as $2220 in transaction fees to make sure that they take the first bite of the pie. Afterward, they mostly sell these tokens at a premium to turn in a profit.

Network Congestion: The increased amount of activity during ICOs causes a huge strain in the blockchain and may result in a bottleneck. During the Status ICO, when they raised a $100 million, there was so much backlog in the network that many people, who wanted to invest in Status, saw their transactions fail.

Storing the tokens: There is a chance that you will not be able to store some of the tokens in any of your crypto-wallets. You can store any tokens made in Ethereum in your ether wallet but tokens made outside of Ethereum can be very complicated to store.

Government intervention: This is where it gets scary. Because of the increased number of scams and a huge amount of unregulated money, various governments may simply decide to start regulating the ICOs. If this happens then this truly could be the death of cryptocurrency. The whole point of cryptocurrency is the idea of decentralization and being outside of government control.

Conclusion

ICOs are going to continue being a part of cryptocurrency and blockchains. We simply cannot overlook the good that they have done. From giving birth to innovative technologies like Ethereum and Golem to giving DAPP developers, around the world, an incentive to innovate and come up with newer and more exciting technologies, their contribution simply cannot be understated.

Having said that though, there is no doubt that ICOs can be a “necessary evil”. Human tendency is to exploit any loopholes for their selfish benefits and ICOs seem to be the tool of choice for many corrupt individuals. Looking forward, what we can all do is act more responsibly and do our own research. Study the white papers, interview the team involved with the specific projects that are up for ICOs and then invest your money.

The Science Behind Cryptocurrencies Cryptography

In this guide, we will be going deep into symmetric and asymmetric cryptography and the science behind cryptocurrencies cryptography.

Cryptocurrencies like Bitcoin and Ethereum use a peer-to-peer decentralized system to conduct transactions. Since the entire process is online, there are fears that the transactions maybe volatile and hackable. What we are going to see in this guide is how cryptocurrency uses cryptography to make their transactions extremely secure.

Digital Signatures

It should provide verification. The signature should be able to verify that it is you who actually signed the paper.
It should be non-forgeable. No one else should be able to forge and copy your signature.
Non-repudiation. If you have signed something with your signature, then you should not be able to take it back or claim that someone else has done it instead of you.

Cryptography gives us a solution to this by means of “digital signatures” which is done via the use of “keys”. So, what are keys? And how are the used in the blockchain? Before we explore those, it is important to know more about basic cryptography.

Save

What is Cryptocurrencies Cryptography?

Cryptography is a method of using advanced mathematical principles in storing and transmitting data in a particular form so that only those, for whom it is intended for, can read and process it. Cryptography has been used for thousands and thousands of years by people to relay messages without detection. In fact, the earliest use of cryptography was seen in the tomb taken from Old Kingdom in Egypt circa 1900 BCE. Cryptography has existed in the modern society through one way or another.

Encryption is one of the most critical tools used in cryptography. It is a means by which a message can be made unreadable for an unintended reader and can be read only by the sender and the recipient. In modern technology, there are three forms of encryption that are widely used, symmetric cryptography, asymmetric cryptography, and hashing.

Symmetric Cryptography

Symmetric cryptography is the earliest known cryptographic method known to man. The concept is very simple and if we were to break it down to steps, this is what it will look like:

You have a message M that you want to send over to your friend.
You encrypt the message with a Key and get a cipher text C.
Your friend gets your cipher text C.
She then decrypts the cipher text using the same Key to retrieve message M.

If we were to show a visual representation of the process, this is what it will look like.

Save

Image credit: SSL2BUY

The are two types of symmetric cryptography:

Stream Ciphers.
Block Ciphers.

What is stream ciphers?

Stream cipher basically means using a fixed key which replaces the message with a pseudorandom string of characters. It is basically the encryption of each letter one at a time.

We are going to discuss 3 kinds of stream ciphers in this guide to give you an idea of how stream ciphers work:

One-time pad with alphabets.
One-time pad with XOR gate.
Linear feedback shift register.

One-time pad with alphabets

For doing this encryption we need to have a key which has the same number of characters as the message and it must be used one time only (hence the term “one-time pad”).

Suppose for this example we are going to send a message, “MEET ME OUTSIDE” to our friend Bob. But we don’t want anyone intercepting our message. This is why, Bob and us have decided to use a one-time pad which goes like this:

“B D U F G H W E I U F G W”

As you can see, the pad has the same number of characters as the message as well, i.e. 13.

Now, this is a very simple example of the one-time pad, we are using this because we feel it is the best example to use to understand this tactic.

Now, one more thing you need take note of, every alphabet will be replaced by its numeric equivalent in during the process.

The numerical mapping goes like this:

The Science Behind Cryptocurrencies Cryptography

Save

During the process, there will be 6 pieces of data that we need which are: Basically, the numerical equivalent of each alphabet. Ok, now that we have built the foundations, let’s move on to the actual process.

Original Message (OM): The original message that we are passing through. In this case “MEET ME OUTSIDE”.
Numerical Original Message (NOM): The numerical equivalent of the original message,
OTP: The One-time Pad.
Numerical OTP (NOTP): The numerical equivalent of the OTP.
NCT: The numerical cipher text which is NOM+NOTP mod 26
CT: The cipher text which is the alphabetical equivalent of the numbers in the NCT.

So, we need to send the message “MEET ME OUTSIDE” and we need to use the one-time pad to encrypt it.

The encryption process

So, let’s start off by putting in the message in the OM

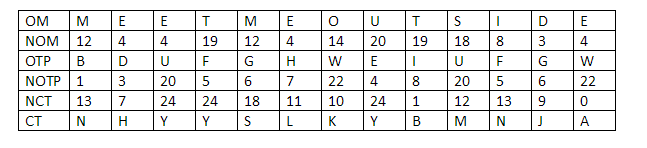
The Science Behind Cryptocurrrencies Cryptography

We put the message “MEET ME OUTSIDE” in the OM row.Ok, so what happened here?

Next, we used the numerical mapping table to get the numerical equivalent of each alphabet. So, let’s refer to the mapping table and see what we get:

Save

In the OTP row we put in the key that we were already given which is, in case you have forgotten, “B D U F G H W E I U F G W”.It’s just simple substitution, we will take these values and put it in NOM row.

Now, in the NOTP row we used the same number mapping table and found the equivalent numerical values of the key which are:

“1, 3, 20, 5, 6, 7, 22, 4, 8, 20, 5, 6, 22”.

In the new row, for the Numerical cipher text (NCT) we add the NOTP and NOM and mod the result by 26 to get our NCT.

Save

So, finally the message “MEET ME OUTSIDE” turns into a pseudo-random series of characters “N H Y Y S L K Y B M N J A”.That’s how you find the values for NCT and then you use the mapping table and find the corresponding alphabets which are: “N H Y Y S L K Y B M N J A”.

That is how the encryption process works.

The decryption process

Now we will see how we can decrypt the message using the exact same key.

Let’s see the data that Bob has with him:

He has the encrypted message that he has gotten from me.
He has the key that both of us share.
He has the mapping table to find the numerical equivalents.

So, how will he decrypt the message using this data?

He will map the numerical values of both the key and the encrypted message to get NCT and NOTP.
He will then calculate the NOM (Numerical value of the original message) by doing this calculation: NOM = NCT – NOTP mod 26.
He will use the mapping table to retrieve the corresponding alphabets.

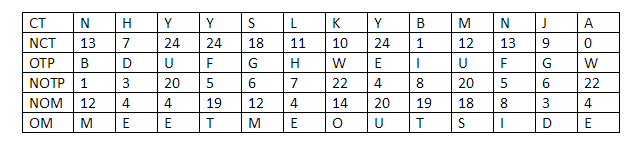
So, let’s see how the NOM calculation work?

Now, if we map the NOM to its alphabetical equivalent using the mapping table then we get:

“MEET ME OUTSIDE”

And just like that, the message is encrypted and decrypted using the same key.

One-time pad with XOR gate

XOR or “Exclusive OR” is a logic gate. What is a logic gate? A logic gate usually takes in 2 inputs and gives out 1 output. The inputs and outputs are binary values, meaning they can be 1 or 0. A XOR logic gate takes in 2 binary inputs and gives out a high output ONLY when the inputs are different. Meaning, if A and B are inputted to a XOR gate then the out C will be 1 ONLY when A is not equal to B.

The XOR gate looks like this:

Save

Image courtesy: Wikimedia

This what the XOR truth table look like:

The encryption process

Suppose you have a plain text data which you want to send to your friend Alice. First, you’ll convert it to its binary form. Suppose the message that you have is this: 00011110

Now you have the key, the key that you share with your recipient and suppose you have passed the key through an algorithm which gives you the equivalent binary result: 01001010.

So now that you have the key, you are going to XOR each corresponding individual bits to get the resulting cipher text output.

Cipher Text = Plain Text XOR Key

So if you XOR both the data the key that you will get is:

“01010100”

This is the cipher text that Alice will get from you.

The decryption process

So now, how will Alice decrypt your message and retrieve the original one?

This is the data that she has:

The cipher text
The key.

So what is she going to do? It is simple.

She will simply XOR the key and the cipher text and she will retrieve the original message! See for yourself:

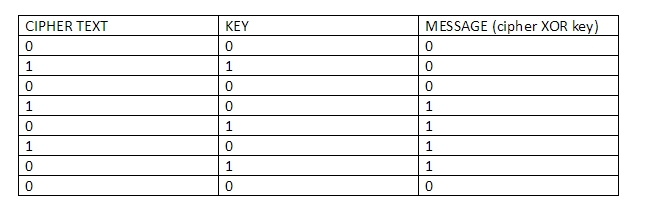
And just like that, she will retrieve the original message.

Linear feedback shift register

What is a linear feedback shift register? It is a function whose future output completely depends on its earlier (or current) state. This will become clearer as you keep reading so don’t get scared off!

The idea of this style of a stream cipher is to predetermine a key with your recipient which will be a linear feedback shift register function which will be used by you to determine the code. Suppose you spoke to your friend Bob and determined that this is the formula that you both want to go with (credit to Daniel Rees from Youtube for this formula).

E(i+3) = E(i+1) + 2E(i+2) mod 26.

And let’s also assume that prior to sending this message you and Bob determined that E(1) = 2 and E(2) = 4.

Now you can see that in this equation, all future outputs are dependent upon the previous outputs.

So, suppose the message that you want to send to Bob is “MEET ME”. Since there are 6 characters, we need to determine 6 values of E() to act as key. We already have predetermined the values of E(1) and E(2). Now we need to calculate E(3) to E(6).

E(3) = E(1) + 2E(2) mod 26 = 10.
E(4) = E(2) + 2E(3) mod 26 = 24.
E(5) = E(3) + 2E (4) mod 26 = 6.
E(6) = E(4) + 2E(5) mod 26 = 10.

So, now that we have the keys, let’s start the decryption.

The encryption process

So now that we have the key and message, let’s create the table:

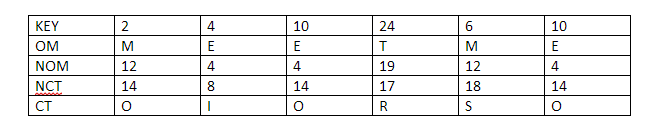
To get the numerical cipher text, you add the key and the corresponding numerical value of the alphabet that you map from this table that we have already seen before:

Save

Now, to get the numerical value of the cipher texts, add the key and the numerical value of the original message and mod with 26.

So you get:

Now use the mapping table again to find the corresponding alphabets and you get “OIORSO”. That’s the encrypted message.

The decryption of this message is really hard especially if you don’t have the key. An expert might spot a pattern though. You will need computers to beak this code.

Examples of Stream Ciphers used in the real world.

The Rivest Cipher 4 of the RC4

Used in WEP aka wired equivalent protocol for wireless network security.
Also an option in TLS/HTTPS for encrypting web traffic.
Since it has been cracked so many times it is not recommended for use anymore.

The A5/1

Use for encrypting GSM (Global System for Mobile communication) phone data and communication.
Edward Snowden in his leaks revealed that the NSA routinely keeps breaking GSM for surveillance purposes so it is not a secured mode of encryption anymore.

So, that is pretty much it about stream ciphers, time to move on to block ciphers.

What is block ciphers?

Block ciphers are a form of symmetric cryptography which uses a key of a fixed length to encrypt a block of fix length. Let’s start by checking out a very common substitution cipher that you must have seen before:

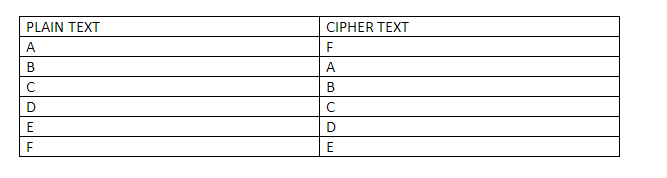
So, if someone were to tell you that they got a message which says “EFBD” and wants you to decrypt it and get the original message instead, how will you do it?

You will simply see the table, see which alphabets correspond to which and then simply substitute right? So “EFBD” is the cipher for “FACE”.

Now let’s check out the plain text and the ciphertext and compare them:

Plain: A B C D E F
Cipher: F A B C D E

So, as you can see, the cipher text is basically the plain text shifted the right by one. So, in this particular case:

EFBD = FACE shifted by 1

That, in essence, is what a block cipher is. Given an input plain text and a key it can generate a unique cipher text. One more thing that is extremely important and should be noted. Given the key, anyone can decipher the cipher text from the plain text and vice versa. The examples that we are giving here are all extremely simplistic, the block cipher happens with HUGE chunks of data.

If we are looking for a visual representation of a block cipher the this is what it will look like:

Another interesting property of the block cipher is that if the key changes then that changes the output cipher text pretty drastically. Let’s do a test with the data we have right now.

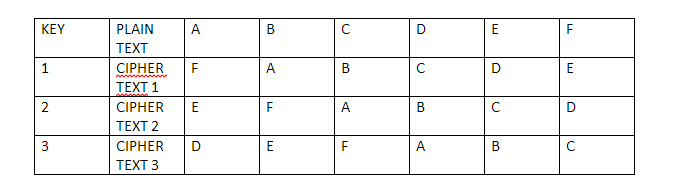
Now, we have 3 keys for the 3 different cipher texts.

In cipher text 1 we are shifting to the right once.
In cipher text 2 we are shifting to the right twice.
In cipher text 3 we are shifting to the right thrice.

So, let’s see what happens when we parse the input “FACE” through all these different ciphers.

When key =1, FACE becomes EFBD
When key = 2, FACE becomes DEAC
When key = 3, FACE becomes CDFB

As you can see, the output cipher text changes everytime you change the key. In the example we have very little data, imagine doing this with HUGE amounts of data, the output will change drastically every single time.

There are two rules for a block cipher to be considered valid:

You must be able to derive the plain text from the cipher text and vice versa given a key.
The function must be efficiently computable.

There is one more important thing that you need to take note of when it comes to block ciphers. The block sizes are fixed so the input plain text needs to be of the same size as the block size. If the input is bigger than the block then it needs to break down to get the correct size, if the input is smaller, then it needs to be padded with some junk data to fit the block size.

Examples of block ciphers

Data Encryption Standard (DES)

Block sizes of 64 bits.
Key size of 56 bits.
Was the government standard till 2001.

Advanced Encryption Standard (AES)

128 bit blocksize.
128, 192 or 256 bit key size.
Considered very secure and widely used nowadays

The advantage of symmetric cryptography

Even though symmetric cryptography has some major problems (which we will discuss in a bit) the biggest advantage of symmetric cryptography is that it requires very little overhead. You just need to share one single key with your recipient to go forward with this method.

Even now, a lot of software use this method in conjunction with asymmetric cryptography to provide fast and efficient encryption/decryption services.

The problems with symmetric cryptography

Even though the overhead is significantly lesser, there are a lot of problems with symmetric cryptography.

Problem #1: The shared key

The fact that the encryption and decryption is done with one single key is a huge problem. First and foremost, the sharing of the key needs to be done in a very secured manner, if anyone gets hold the of key then all your data will be compromised.

Problem #2: It is not scalable

Another huge problem with symmetric cryptography is that it is not scalable at all. Suppose Alice runs an information center and sends data via symmetric key cryptography. It’s ok if she is only dealing with 3-4 clients. But the most clients she gets, the more unique public keys she will have to handle and take care of. Eventually, it will become too much to handle.

Because of these vulnerabilities of symmetric key cryptography, a solution was needed, and in the 1970’s it finally came.

James Ellis’s breakthrough

In 1970, British mathematician and engineer James Ellis thought of an idea which was based on a simple concept. What if encryption and decryption were inverse operations based on 2 different keys? In traditional cryptography i.e. symmetrical cryptography, the message had to be sent along with the key to the intended person for them to decrypt the message, but this presented the very real idea of an attacker getting their hands on the key.

Ellis envisaged that the receiver of the message couldn’t be a passive party, and they had to have a “padlock” and a “key” for themselves. The padlock could be sent to anyone in the world but the key had to be kept private. So, anyone can send a message to the receiver by locking it with their padlock and since only the receiver has the key, only they can open it.

Now, this was the theory, there needed to be a practical form of this theory, and that came because of two brilliant principles:

The trapdoor function.
The Diffie–Hellman key exchange.

What is the trapdoor function?

A trapdoor function aka a one-way function is a function where it is easy to go from one state aka the domain to the other state aka the range but it is hard to go back from the range to the domain unless you have knowledge of a key which is called the trapdoor function.

Diagrammatically it is represented like this:

Image credit: Cornell.edu

The trapdoor functions are based on the idea of keys. Wherein the public key (K) is used to go from the domain to range. In order to come back to the domain from the range we have to use a trapdoor function which is also known as the private key (k). It is also implied that the private key and public key are mathematically related to each other and also they have to related to each other via another trapdoor function f() such that K= f(k) so that the private key is infeasible to be determined by the public key .

A simple example of this is a multiplication of large numbers. Suppose you have two numbers 171 and 118 then it is simple to determine that 171 * 118 = 20178. However, if you just know 20178 then it is hard for you to determine what the initial numbers were unless you have a key with you, in this case the knowledge of just one of the two numbers, to determine the second one.

What is the Diffie-Hellman key exchange?

Suppose, there are two people Alice and Bob and they want to attack a bank. However, they are on either sides of the bank and they can only communicate with each other via a shared line which is being tapped by the bank.

Save

Something like this.

Keep in mind, everything that Alice and Bob say to each other will be eavesdropped upon by the bank. So, how can they both decide on a date to attack the bank without the bank getting to know about it and without Alice and Bob explicitly exchanging that information?

This conundrum can be answered by the Diffie-Hellman key exchange; it is a concept by which two parties can get hold of secret information without sharing it.

To understand how the Diffie-Hellman works, we need to use one of the most famous applications of this theory, the secret colour exchange.

For this there are 3 things that you need to keep in mind:

Alice and Bob both publicly agree that yellow is going to be the common paint that they are both going to use.
Alice then secretly keeps to herself that she is also going to use orange along with yellow.
Bob secretly decides that he is going to use aqua along with yellow.

Stage One

Since it was publicly declared that yellow is going to be the colour of choice:

Bank: Has Yellow
Alice: Has Yellow
Bob: Has Yellow

Stage Two

Now Alice mixes in her private colour aka orange with yellow and gets a composite colour which we will call CA.

At the same time, Bob mixes his private colour aqua with yellow and creates composite colour CB.

So, at the end of stage two this is what things look like:

Bank: Yellow
Alice: CA
Bob: CB

Stage Three

Now, Alice and Bob will send each other their respective colours, which will promptly get tapped by the bank. However, the bank now faces a problem.

Colour combinations are a trapdoor function.

While it is easy for someone to combine two colours and generate a third colour, it is infeasible for them to determine the first two colours from the given third colour. So, the bank will get hold of CA and CB but will have no idea which are the colours that has gone into its creation.

So, this is what things are looking like right now:

Bank: Yellow, CA, CB.
Alice: CB
Bob: CA.

Stage Four

Now, Alice and Bob are once again going to mix their secret colours into the mix that they have received from the other person, so now both of them are going to have a mix of yellow, orange and aqua which is brown. The bank, however, will only have CA and CB because they have no idea what the secret colours are.

So, this is what things look like now:

Bank: Yellow, CA and CB.
Alice: Brown.
Bob: Brown.

And this is where the trick lies, by not revealing their secret colours, both Bob and Alice have, in their possession, the colour brown, even though they never explicitly exchanged brown with each other.

This is what the diagram of this entire exchange looks like:

Save

Image Courtesy: Wikipedia

This is the representation of the Diffie-Hellman exchange, but a mathematical means was needed to make sure that there could be practical applications of this as well. For this reason, the modulus function was used.

The mathematical form of the Diffie-Hellman exchange

Suppose there is a generator g for a finite field of size n. And in that field, we choose two random values a and b. It will be hard for an attacker to determine g^ab given only g, g^a and g^b. This is the condition which activates the trapdoor function. Given this condition, two parties can exchange messages and reach the same conclusion without explicitly communicating it with each other.

So, mathematically this is what happens.

Alice chooses a random value “a” from the field n and determines a message M1 such that:

M1 = g^a mod n.

Similarly, Bob chooses a random value “b” from the field n and creates message M2 such that:

M2 = g^b mod n.

Both Alice and Bob can now relay the message to each other.

Alice now determines special message K by doing the following:

K = M2^a mod n= g^ab mod n.

Bob now determines the same message K by:

K = M1 ^ a mod n = g^ab mod n.

So, both Alice and Bob reached the same conclusion without explicitly sharing this information.

This Diffie-Hellman key exchange was invaluable in the formation of asymmetric cryptography:

What is asymmetric cryptography?

Asymmetric cryptography utilizes two keys, a public key and a private to encrypt and decrypt a particular data. The use of one key cancels out the use of the other.

The diagrammatic representation of it looks like this:

Save

Image courtesy: SSL2BUY

There are two real world use of asymmetric cryptography that we will look into in this guide and both are important for their own reasons:

The Rivest-Shamir-Adleman algorithm aka the RSA.
The Elliptical Curve Cryptography.

What is the RSA algorithm?

The RSA algorithm is the most widely used and popular asymmetric cryptographic algorithm in history. It is named after MIT professors Rivest, Shamir and Adleman who discovered this algorithm. Now, how does it work? The idea is derived from the breakthroughs that Diffie-Hellman had.

So, these are the variables that we will work with:

Suppose you have the secret message “m”. “m” raised to the power of a random number e and then the modulus of that with a random number N will give you the cipher text c.

Basically. m^e mod N= c

Take note, it is EASY to perform this function to get the output c BUT given only c, e and N it is difficult to get the message “m”. It will require a lot of trial and error. This is the one-way trapdoor function that we will apply to find “m”.

But now, the idea of the trapdoor function is to have a key which will make the reverse process (the decryption) simple for the recipient. So, for that we will need to find a random variable “d” which will make this process possible:

c^d mod N = m.

Now keep in mind, c = m^e mod N, so on substituting.

m ^ e ^ d mod N = m.

m ^ ed mod N = m

So, in the above equations:

Public key = e and N.
Private key = d.

Now, before we even begin to see the method behind the madness, let’s do a simple calculation to see how the entire process works. (Shout out to Anthony Vance’s youtube channel for this example).

Suppose the message that you have to send is 42. In other words, m=42.

Along with that:

e = 17.
N = 3233.
d = 2753

The encryption process

c = m^e mod N.

Using simple substitution:

c = 42^17 mod 3233 = 2557.

So the cipher text is 2557.

The decryption process

Let’s do c^d mod N.

2557^2753 mod 3233

This gives us the value of m that is 42.

Genius isn’t it?

Now, remember when we talked about trapdoor functions we came to the conclusion that private and public key needs to be mathematical derivatives of each other in a way that:

F(private key) = public key, where F() is another trapdoor function.

It should be difficult for anyone to determine the private key from the public key. In fact, it should be so difficult that it will take the world’s most powerful computer decades upon decades to derive one from the other.

To answer this conundrum, we go back centuries and meet our next genius, Euclid.

Euclid and prime factorization

Euclid found out centuries ago that any number > 1 can be written as a product of prime numbers.

Eg. 15 can be written as 5*3.
255 can be written as 5*17*3.

Let’s go back to our two equations:

C= m^e mod N.

Here, N is the key in the trapdoor function. While N maybe publicly known it should be hard to determine prime factors that make up the number N. If you know the prime factors, then it is child’s play to discover the product N.

Eg. You can use your web browser to multiply two huge numbers and find the product in less than a second:

Save

It took less than a second, 0.22 seconds, to do the calculation. And the bigger the number gets, it will take a little more time, but still, the calculations will be done super fast.

However, if you input a huge number and ask your computer to find its prime factors then it may take days, months and even years to find the prime factors.

This is the trapdoor function that cryptographers used to determine the value of N. This is basically, the heart of the trick.

This is what you have to do to use RSA algorithm:

First, generate a big random prime number P1.
Generate a second big random prime number P2.
Find N by calculating P1 and P2.
Hide the values of P1 and P2 and make N public.
N should be a huge number and it will take the most sophisticated machines in the world decades to find the values of P1 and P2.
So to summarise, N is the trapdoor and its prime factors P1 and P2 are the keys to the trapdoor.

Ok, so now we have determined how N is calculated and the trapdoor that works in it. But we still haven’t determined the value of “e” and “d” and we still haven’t seen how the private key is derived from the public key. In order to generate all these remaining values, we need to find a function that depends on knowing the factorization of N. And for that we need to go and visit our next genius, Leonhard Euler.

Euler and breakability

In 1760, Swiss mathematician Leonhard Euler did some path breaking studies. He studied the nature of numbers and more specifically the breakability of the numbers which he called the phi function.

Basically given phi(N) where N is a random integer, the value of N will be the number of numbers between 1 and N which do not share any common factors with N.

So, if N is 8 then:

The numbers between 1-8 are: 1,2,3,4,5,6,7 and 8.

Among these numbers, only 1,3,5 and 7 don’t share any factors with 8 except 1.

Meaning, phi(8) = 4.

Now, calculating the phi function is difficult except for one case. To know this, check out the following graph. The graph tracks the distribution of phi values over integers upto 1000.

Save

Image courtesy: Khan Academy

See that straight green line at the top which is conveniently arranged? That is the phi of prime numbers. Since the definition of a prime number is that it is unfactorizable apart from by itself, for any prime number p the phi(p) = p-1.

Let’s see this in practice. Suppose you have a prime number 7.

The numbers between 1 and 7 are: 1,2,3,4,5,6,7.

The only number that shares a factor with 7 in this series is…7!

So the phi(7) = 6.

Similarly, if you were to find the phi of a large prime number say 541 then:

Phi(541) = 541-1 = 540.

It becomes very simple to calculate the phi for a prime number. And this gains, even more, significance when you consider the multiplicative nature of phi functions. What is the multiplicative nature of phi functions?

For any two numbers A and B:

Phi(A*B) = phi(A) * phi(B).

Now, let’s go back to algorithms. Alice has determined two large prime numbers P1 and P2 and has determined a number N by doing P1 * P2.

So, using the multiplicative property of phi functions:

Phi(N) = phi(P1) * phi(P2).

Phi(N) = (P1-1)*(P2-1).

And just like that, we have discovered the trapdoor function for phi. If we know the prime factors of N then it is easy to calculate the phi(N).

For eg. the number 77 has prime factors 7 and 11.

So phi(77) = (7-1)*(11-1) = 60.

It becomes very easy when you know the prime factors of N.

Now, one final bit of mathematical wizardry was required. We have the phi function and we have the modular exponentiation functions that we have determined before, we need to bring these two together in one neat equation.

And for this, we turn to Euler for help once again.

The Euler’s theorem

Euler’s theorem states that:

For any two numbers m and n that don’t share a factor:

m ^ phi(n) ≡ 1 mod n

Meaning, for any two numbers m and n, as long as they don’t share a factor, m raised to the phi(n) divided by n will always leave a remainder of 1. Let’s see this in an example.

Suppose, m= 8 and n = 5.

Phi(5) = 4

So, 8 ^ 4 = 4096.

Replacing this in the Euler’s theorem equation:

4096 ≡ 1 mod 5 holds true because 4096 on being divided by 5 leaves a remainder of 1.

Now, the equation: m ^ phi(n) ≡ 1 mod n needs to be modified a little bit before we get our final solution.

Modification #1

1^k = 1 for all k.

So, keeping this in mind, if in m ^ phi(n) ≡ 1 mod n we multiply the exponent phi(n) with any number k, the final solution will be 1^k which is still 1.

Now, this modifies the equation like this:

m ^ k*phi(n) ≡ 1 mod n

Modification #2

For all m, m*1 = m.

So, in our modified equation, if we multiply both sides by m we get:

m*m ^ k*phi(n) ≡ m*1 mod n

Which becomes:

m ^ k*phi(n)+1 ≡ m mod n

Now, this is the final form of our equation.

Before we proceed, let’s bring back the old equations to refresh our memory:

c = m^e mod N.
m = c^d mod N
m ^ e*d mod N = m

Now, checkout the last equation doesn’t that look similar to our new modified equation:

m ^ k*phi(n)+1 ≡ m mod n

And this is the breakthrough.

On comparing the two equations, we get:

e*d = k*phi(n) + 1

We FINALLY have an equation where the value of e and d depends on phi(n).

Now, since we already know the value of e, it is easy to calculate d, the private key, ONLY if the factorization of N is known (which is a secret that Alice has kept to herself).

So, d= (k*phi(n) + 1)/e.

This is the trapdoor that will undo the encryption done by her private keys e and n.

Example to see how this all works

Suppose Bob and Alice are exchanging messages.

Bob wants to send a message M to Alice where M=89.

Now, Alice needs to generate her keys.

She uses to prime numbers p1 and p2 where:

P1 = 53.

P2 = 59.

N = P1 * P2 = 53 * 59 = 3127.

Phi (N) = Phi(P1) * Phi (P2) = (P1 – 1) * (P2 – 1) = 52 * 58 = 3016

Now, she needs to generate a value e which will have no factors with the value of phi(N).

So, she decides e = 3.

Now, she will generate her private key d:

d = (k*phi(N) + 1)/e

Taking k = 2 we get:

d = (2* 3016 + 1) / 3 = 2011.

Now, she will lock up all the values except N and e which are her public key and make the knowledge of these two global.

Bob encrypts the message

Now, Bob needs to send message M, which is 89, and he needs to calculate the cipher text c such that:

c = M^e mod N.

Now, we know that: M = 89, e = 3 and N = 3127.

So: c = 89^3 mod 3127 = 1394.

He then sends it over to Alice.

Alice decrypts the message

Alice gets the cipher text and all that she has to do is to decrypt it using her private key d which we know to be 2011.

So, Alice does this calculation: c^d mod N

1394^2011 mod 3127 which is 89 aka the original message M.

And this, is the RSA algorithm, the most widely used cryptographic algorithm

What is elliptical curve cryptography?

Elliptical curve cryptography is what is used by bitcoin, ethereum etc. for their encryption purposes. So what is an elliptical curve? An elliptical curve is any curve that satisfies the following equation:

Y^2 = x^3 + ax + b

Where (x,y) is a point on the curve and a and b are constants.

There are infinite curves that you can make. The following is how one of these curves, in general, look like:

Save

Image credit: CSBreakdown youtube channel

What are the properties of an elliptic curve?

The curve is symmetric across the x axis.
Any line that goes through 2 points on the curve will intersect the curve on a third point.
Any tangent on the curve will intersect the curve on one more point.

Performing maths on the curve.

Addition property of the curve

Suppose there are two points on the curve V and A. Let’s trace those on the curve and put a line through them. This will intersect the curve on a third point.

Save

Image credit: CSBreakdown youtube channel

We will call this third point X, and we will reflect it on the curve like this:

Save

Image credit: CSBreakdown youtube channel

The reflection of X is a point which will incidentally be (V+A). This is the additive property of the elliptical curve.

Interesting note. If we add two reflections with each other aka if we were to add X and V+A in the graph above, we will get infinity. The reason for that is that the line through X and (V+A) will intersect the curve at infinity.

Multiplication property of the curve

Now, what if we want to add a number to itself? Like suppose we have a point V, what do we do to find 2V? We will run a tangent through V and intersect it at a point in the graph and then find the reflection of the point on the curve. That reflection will be 2V.

Save

Image credit: CSBreakdown youtube channel

This is also the multiplicative property of the graph because we are finding points which are basically the multiplication of an integer with the point itself. Now suppose we want to find 3V. We will join V and 2V and then reflect the point of intersection, like this:

Save

Image credit: CSBreakdown youtube channel

You see how the points cycle across the graph? This is what gives it its security.

Mathematical properties of an elliptical curve

Property #1: The points on the curve form an Abelian group

The properties of the Abelian group are as follows:

They have identity.
The have inverses aka reflections.
The points are associative meaning for three points A, B and C on the curve: (A+B) + C = A + (B+C).
The points are closed on the curve.
The points are commutative meaning for two points A and B. A+B = B+A.

Property #2: Multiplication on the curve is fast

All multiplication done on the curve can be done very fast. Now suppose we have a point P and we want to find 100P. Instead of adding the number to itself 100 times we can do the following:

Add the point P to itself to get 2P.
Add 2P and P to get 3P.
Add 3P to itself to get 6P.
Add 6P to itself to get 12P.
Add 12P to itself to get 24P.
Add 24P and P to get 25P.
Add 25P to itself to get 50P.
Add 50P to itself to get 100P.

So, instead of going through 99 steps you cut short the entire thing to just 8 steps.

Property #3: Division on the curve is slow

Whilst multiplication is fast, the division is very slow. Suppose we have Q = nP and we want to find the value of n by dividing Q by P. We can’t really do that. We will have to manually go through the numbers one by one to find a value which satisfies the equation. This makes it very slow. This is called the discrete logarithmic problem and this is what gives the curves its trapdoor function i.e. it is easy to multiply n and P to get Q but given Q and P it is infeasible to get n.

The elliptical curve Diffie-Hellman key exchange

So, till now we have seen the various properties of the curve and we have also seen that the curve has a trapdoor function. Now how do we determine whether it is usable for cryptography or not? Let’s test it out with the Diffie-Hellman key exchange. Suppose we have Alice and Bob and they want to both come up with a common secret without anyone knowing what it is and without explicitly exchanging its information with one another. How will they do that via elliptical curves?

Firstly, they will publicly agree on a curve to use and a point P on the curve. This will be public knowledge and available to everyone.
In secret, however, Alice will choose a secret point “a” and Bob will choose a secret point “b”.
Alice will compute “aP” and send it over to Bob. Anyone can intercept this message, however, even with the knowledge of P they will never be able to determine the value of “a” because, as we have already determined, there is a trapdoor function which will make division infeasible.
Similarly, Bob will come up with the value “bP” and send it over to Alice.
Alice will then multiply her secret key to the message that she gets from Bob to get a(bP). Bob will do the same and come up with b(aP). Since all the points on the curve are Abelian: a(bP) = b(aP). And just like that, they have come upon a secret shared information.

So as we can see. The curve satisfies the Diffie-Hellman key exchange.

So how does signature verification work on the elliptical curves?

(Note: This is what specifically happens in bitcoin)

Before we see how the process works let’s checkout certain variables and their meaning that we will be using the following equations.

Private key = d.
Message = z.
Public key = Q.

G will be a constant point on the graph which will be provided by bitcoin.

“k” is a random number which will be generated automatically for every unique signature.
“n” is another constant that will be provided by Bitcoin.

Ok, so now let’s see how the maths behind the verification work.

Signing a message

Public key Q = dG. (it is impossible to get the private key from Q and G because division in infeasible).

Now we will multiply the G with the random number “k” and plot that point on the graph. The co-ordinates of that point are (x,y). i.e. (x,y) = kG

Next, we determine two values r and s such that:

r = x mod n.

s = (z + rd) k^-1 mod n

The reason why we generate r and s is because these are the co-ordinates of our signature.

So, we send the point (r,s) for verification.

Verifying a message

The verifiers will conduct a simple equation:

z*s^-1*G + r*s^-1*Q

The value of this equation will give us the point (x,y).

Now, the verifiers can simply compare the x co-ordinates. They don’t have the x co-ordinate given directly to them from the sender BUT they have the values of r and n.

And as we already know that r = x mod n, and then they can simply solve for x.

If the values of x match out, then this means that the signature is verified!

Bonus: A deeper look into the maths

Let’s check out the equation that the verifiers will have to do once again:

Step 1: z*s^-1*G + r*s^-1*Q

We know that Q = d*G, let’s simply substitute the value.

Step 2: z*s^-1*g + r*s^-1*d*G

We can take (z + r*d) common

Step 3: (z + r*d)*s^-1*G

Now remember, we have already established that s = (z+r*d)*k^-1 mod n ,let’s substitute the values here:

Step 4: (z+r*d)*(z+r*d)^-1*k*G

The (z+r*d)*(z+r*d)^-1 cancel each other out and we are left with:

Step 5: k*G which is the co-ordinate (x,y) that the sender originally sent.

What could go wrong in Elliptical curves?

While it goes without saying that elliptical curves are the best mode of cryptography out there, the fact remains that it still has few vulnerabilities:

What if a wrong curve was chosen? If the curve has a loop in it then there is a possibility that 1001P = P for any point P on the curve.
A weak curve maybe is chosen which can be broken into.

It has its weaknesses but they are pretty manageable weaknesses.

RSA vs EEC. Why did bitcoin and ethereum go with elliptical curves?

The reason why EEC was chosen over RSA is because it offers the same level of security as RSA by consuming far less bits. Eg. for a 256-bit key in EEC to offer the same level of security RSA will have to provide a 3072-bit key. Similarly, for a 384-bit key in EEC the RSA will have to provide a 7680- bit key to provide the same level of security! As can be seen, EEC is far more efficient than RSA.

Fun Fact: The NSA has declared that a 384-bit key in EEC is strong and secure enough to encrypt top level secret documents.

How do the keys work in blockchain?

As mentioned above, bitcoin and ethereum use elliptical curve cryptography. So, what happens when someone sends you money on the blockchain? They send you the money to your public address which is basically the hash of your public key and some additional information. As we have seen above, the public key is derived mathematically from your private key.

Public and private keys are both large integer values and they are represented, for brevity’s sake, via the Wallet Import Format (WIF) which consists of letters and numbers. A sample private key and public address looks like this in WIF:

Obviously, you shouldn’t share your private key with the world like we just did! The private key is used to sign off on the transaction that the user wants to do. So, if someone has access to your private key, they can sign off on transactions using your private key and, in essence, steal from you. Also, as you can see, the private key is longer than the public address.

So, how is a public key derived from the private key in the blockchain? Let’s take the example of bitcoin for this specific example.

Suppose, Alice wants to generate her keys so that she can conduct transactions on the blockchain. This is what she will do:

First, she will generate her 256-bit private key. She can either do so manually OR she will use an auto-generator. This is an example of a private address generator that you can find in a wallet-generator.net:
Save
Next, she will have to generate the public address which the algorithm inside that wallet will do automatically by following these steps.
First, her private key will be parsed through the SHA 256 hashing algorithm to get a hash.
Then hash will be parsed through the RIPE MD 160 function and a new hash will be generated and a copy of it will be kept aside, let’s call this PART A.
Then the hash will be hashed through SHA 256 to generate another hash.
Then the new hash will be hashed through SHA 256 again to generate another hash. The first 7 bits of this hash will be saved, let’s call it PART B.
PART A and PART B will be added up and the result is the public address.

It is infeasible for this process to be reversed in a way that the public address can be used to generate the private key. It will take the world’s most powerful computer 40000000000000000000000000000000 years to complete this calculation! Safe to say your address and key are secure.

So how does the signing process work (a simple overview)?

Suppose Alice wants to send 500 BTC to Bob. She will follow the following steps:

She will create transaction and sign it off with her private key.
She will the send the transaction to Bob’s public address.
Bob can then decrypt the message by using Alice’s public key to verify that it was indeed Alice who sent him the bitcoins and the transaction is deemed complete.

If this were to be shown in an image this is what it will look like:

Save

Conclusion

So, as can be seen, public key cryptography aka asymmetric cryptography is one of the backbones of cryptocurrency. It is impossible to even imagine how bitcoin and ethereum would have been secure without it. Every time you make a transaction, be thankful to all the mathematicians and cryptographers who have made this wonderful medium possible.

What is zkSNARKs: Spooky Moon Math

By ảgaergaer Wednesday, October 11, 2017

What is zkSNARKs: Spooky Moon Math